PWM开关变换器分析方法综述--打印文章-电源开发网

【字体：小大】

PWM开关变换器分析方法综述

http://www.dykf.com 2008/11/16 电源开发网

Abstract：Analysis methods of PWM DC—DC converters are introduced in detail in this paper, and continuous analysis method is emphasized on the application。 In addition, the　 development tendency of the analysis method is also presented。

Keyword：PWM switching converters analysis method

1 引言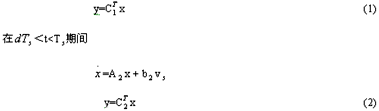

　　近年来，随着开关变换器在理论分析方法上取得了突破性进展，开关变换器的研究在国际上形成了热潮。开关变换器电路以其高效率、体积小、重量轻在各类功率变换电路中占据主导地位。由于PWM型DC--DC变换器是一个强非线性或时变或断续的电路，因此，变换器电路动态特性的分析和设计都较困难。

　　开关变换电路的分析方法有很多[1],大致可分为两类：数值仿真法和解析建模法。数值仿真法是指利用各利用各种各样的算法以求得变换器某些特性数字解的方法。其优点是准确度和精确度都很高，可以得到响应的完整波形，适用范围广，可进行小信号分析和大信号分析，用起来方便；缺点是物理概念不甚清楚，对设计指导意义不大[2]。而解析建模法指能用解析表达式表示其特性的建模方法，建模时常做某些近似假定，以简化分析，它着眼于工作机理的分析，满足一定精度要求下要简单通用，能为设计提供较明了的依据。本文对PWM开关变换器的分析方法作以较全面的综述并总结其发展的趋势。

2 数值仿真法

　　数值仿真法有直接法和间接法。前者直接利用现有的通用电路仿真程序，如SPICE等，不需要重新建立电路模型，只需局部地建立一些专用的仿真模型，等效子电路及子程序即可,其不足之处在于计算速度较慢；后者是指在采用某种数值分析之前，需要从原变换器电路中建立一个专用的数学模型，如离散时域模型等，然后用适当的数值分析法求解，其优点是计算速度较快。

2.1　spice 和pspice 仿真

　　Spice作为一种通用电路仿真程序，在开关功率变换器时域大信号和频域小信号仿真中得到了广泛的应用[3]。其优点是：可分析功率半导体器件、变换器电路、电力电子系统等，可直接由电路仿真，不必列写电路方程, 而且它可以解决大信号分析问题，但难用解析法求解。它还存在着运行时间长、不易收敛等问题。而PSPICE是SPICE电路模拟器家族的一员，是首先用于IBM--PC机上基于SPICE的模拟器。PSPICE和SPICE的主要区别在于PSPICE收敛性和性能更好，但作电路的瞬态分析时，也占用较多机时[4]。

　　SPICE和PSPICE的仿真结果都以数据文件形式表示，可以将它输入其它软件如MATLAB等，以便进一步对电路性能进行评估和寻优。香港理工大学Y.S.Lee等用PSPICE和MATLAB结合，开发了电力电子电路优化用的CAD程序MATSPICE[3]。其用途包括：建立SPICE模型，存储在数据库内；仿真和性能评估；设计目标和约束定义的描述；多目标优化等。

　　另外，由于开关变换器闭环时是强非线性系统，在参数设置不当时易出现混沌类现象，而采用解析法时难以对混沌类现象进行预测，从而更需要借助于数字仿真。
　　
　　SPICE同其它高性能的软件相结合可为功率电子电路和系统的仿真创造更为有利的计算机辅助分析和设计工具，这是其发展的一个重要方向之一[5]。

2.2 离散时域仿真法

　　1979年美国弗吉尼亚电力电子中心李泽元教授首先提出了开关DC—DC变换器的离散时域仿真法。 20世纪80年代后期, 清华大学蔡宣三教授对该方法进行了深入的研究。此法是研究拓扑变化及元件参数变化对系统瞬态特性影响的有力工具。在应用时的基本方法是：列出非线性系统的分段线性方程，求状态转移规律，由此导出非线性差分方程，再用计算机求解。它可用以仿真多环控制系统，实现不同的控制规律，快速、准确、高效率地研究拓扑变化和元件参数变化对系统瞬态特性的影响。还可用以仿真稳态过程、大信号响应及小信号相应。其缺点是，得不到解析形式的数学方程，物理意义不清晰。文献[6]将Ｍ＋Ｎ维的开关电源分解成慢和快两个子系统，分别以大步长和小步长积分，Ｎ维子系统的输出以低阶多项式插值，作为Ｍ维子系统的输入，从而达到了快速性和准确的统一。文献[7]采用截断

　　Taylor级数，但存在时间量化误差。文献[8]采用Chebeyshev级数法计算状态转移矩阵，通过求解一简单的代数方程获得拓扑改变的时刻，克服了文献[7]中存在时间量化误差的缺点。另外，值得提出的一种方法是改进节点法（ＭＮＡ）。它部分的改善了节点法的处理电源不充分、不能包含与电流有关的元件、不便于得到支路电流、难以实现有效的数字积分、分析电路的零极点要用特殊技术等缺点。但仍存在效率低、需要更多电路变量等问题。文献[9]提出一种开关构造函数，以Ｓ域改进节点方程来描述变换器的动态行为，通过拉氏反变换获得时域响应。这种方法中所有的拓扑结构可用一个单一的改进节点矩阵来代替，因而仿真速度快，且没有作任何近似[9]。
　　
　　众所周知，快速性和准确性是现有仿真算法的一大矛盾。因此，如何在这两者之间取得更好的协调和统一，将是数值仿真今后发展的一个重要方向[5]。

3 解析法又可分为离散法和连续法两大类。离散解析法采用差分方程和Ｚ变换技术。其优点是精确度
高，建模时基本不作任何假定，可用于任何开关变换器。但它只能求出控制输出波形函数，且分析程序复杂，所得结果更复杂，很难了解网络的性质，不能处理非理想开关，不能分析纹波。因此近年来离散法发展缓慢，而是朝着离散法与连续法结合的方向发展[10]。

　　连续解析法包括平均法（状态空间平均法、电路平均法）和渐进法。平均法采用微分方程和Ｓ变换的形式，并作一些数学处理，因此模型及结果都简单，但不如离散法精确，且输出纹波无法体现。其本质是平均，平均的目的是将时变电路变为非时变线性电路，在小信号的情况下可线性化，从而能用它来分析变换器的稳态以及小信号时的各种性质，从而线型电路的各种分析设计手段均可套用。

3.1 平均法

　　S. Cuk 和R.D Middle brook在1976年提出的状态空间平均法是目前使用最广泛、最具代表性的平均方法[11]。他们对状态变量进行了平均和线性化处理，给出描述开关变换器电路特性的一般解析式及其规范化化的等效电路形式。对于一个工作在连续导电模式下的PWM型DC――DC变换器，其状态方程分别为

　　这就是著名的状态空间平均法。由上可知, 时变电路(1)(2)变成了非时变电路(3)，从而可求稳态工作点、小信号传递函数等。状态空间平均法是ＰＷＭ开关变换器的一个系统的分析方法，简明精确。但也存在着问题：稳定性分析不准确、不能分析纹波、无法分析准谐振变换器，且线性化方法只是局部处理，故不能用于大信号分析，对方程进行平均就意味着电路不出现高频成分，倘若高频成分起主要作用，则平均结果就不正确。在考虑了实际工作过程中输出反馈控制电路的工作特性对分析结果的影响后，F.C.Ｌee等提出了离散平均方法[12]，对状态进行平均处理而对输出结果进行采样离散化处理，得到了开关变换器电路的更加精确的描述方程和等效电路形式。为了便于计算机辅助分析，A. Pietkietwics 等基于开关变换器电路的拓扑性质提出一种利用节点方程和回路方程的平均方程[13]。但平均的条件是：开关变换器的输出低通滤波器的特征频率远小于开关频率，且电路的输出纹波较小。Brown等提出的抽样序列模型[14]保留了这个高频成分，因此模型更精确。从模型的推导来看，它对扰动不作平均正是保留了高频成分。其优点是提高了稳定性分析的精度，但它引入了冲击函数序列，处理麻烦，反馈网络的设计变得复杂。

　　连续平均法中的另外一种是平均值等效电路法。它是从原变换器出发进行电路处理，最后得出一个等效电路模型。在推导时，只是处理开关元件，而线性元件不变。如P. R. K. Chetty的电流注入等效分析法[15]，等效受控源法以及三端开关器件法[16]，它们都是从电路结构出发，利用时间平均技术而进行电路分析，但当电路元件增多，要得出平均后的拓扑结构需要很大的运算量。

　　围绕着拓扑不变这一要求，有不少处理方法诞生：Wester的电路平均法[17]；Y.S.Lee的MISSCO[18]和许建平的ECA法（Equivalent Circuit Approach），Voperian的简化开关模型（Ｖ模型）[19]以及Tymerski等用谐波平衡原理建立的开关模型（Ｔ模型）。

　　PWM开关模型对常见的开关变换器都适用。而Ｖ模型与Ｔ模型都是基于PＷＭ开关模型的概念。它们都是把开关从电路中独立出来，提出一个PWM开关模型――单刀双掷开关。各端按所接元件性质的不同区分为三个端，分别接三极管、二极管和公共端。它对各类ＤＣ―ＤＣ变换器都适用。忽略电容的损耗电阻时,V模型与T模型推导的出发点相同。对于PWM开关变换器, 都有下式:

　　若对(6)式进行小信号扰动分析即得Ｖ模型。更精确的，将扰动产生的响应分为基波和高次谐波，用谐波平衡原理，则得出Ｔ模型。因而，Ｖ模型是Ｔ模型的特例。两者的区别在于：前者是平均法，后者本质上是谐波平衡法；前者在时域中处理，后者在频域中处理；前者是一线性模型，且模型比较简单，适用于小信号分析，并可分析一些寄生效应；后者是一非线性模型，可用于大信号分析，并可用于波形失真的估计，它的一阶近似就是Ｖ模型。但Ｔ模型只可以考虑单频率的扰动，不能分析多频扰动，而且不能用于可能产生谐波的变换器的分析[20,26]。

3.2 渐近法

　　连续解析法的另一个分支是渐近法。其前提是待解方程存在小参量。一般的，开关变换器的状态方程可写为：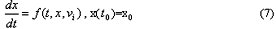

　　x是状态变量，v 为输入。对于理想开关，f有跳跃，但在Caratheoreodory意义下满足

的x仍称为(４)的解[21]。因此，对（7）的求解有可能用渐进法。渐近法有KBM法、Ｖolterra 级数法[22]、多尺度法等。ＫＢＭ法对于分析瞬态过程及纹波颇有成效，常用于分析二阶系统，但是对于高阶系统求解太繁琐，且没将稳态与瞬态分开。另外，对于谐振式变换器的状态方程，无法引入小参量，故不能用KBM法。Ｖolterra 级数法只适于分析弱非线性系统。多尺度法的缺点与ＫＢＭ法相同。另外有一种与渐进法颇为相似的是谐波平衡法，严格上讲，它不是渐进法，因为它不需小参数的存在，但它能估计高次谐波。最后，需特别指出的是丘水生提出的等效小参量法[22，23]，它是近年来发展起来的精度高且分析简单的适于求解强非线性高阶系统的一种符号分析法, 是渐进法的一种[24]。其实质是在谐波平衡法中引入扰动技术，把周期解表达为按等效小参量展开的三角级数，避免求解变量较多的非线性代数方程，因此计算量大大减少，且可以获得闭环系统稳态直流解，占空比、输出纹波的解析解，并能直接说明纹波对占空比的影响及其同开关频率的关系，为设计提供依据。此法已被应用于PWM变换器和准谐振变换器的稳态分析[25，26], 在开关频率较低、纹波较大时仍获得很高的精度。另外此法还被发展, 提出了适合瞬态分析的等效小参量法[27]。目前此法得到了广泛的应用和推广。

4 结语

　　本文对PWM开关变换器的分析方法作了一个较为全面的回顾与总结，对各种方法做了说明和评价。综上可知，离散法的发展缓慢，连续解析法的发展已有一定成效，但有些方法还需提高精度。

参考文献

[1]ENG S C,ORUGANTIR,,LIANG Y C,ET AL. An automated algorrithm for Small　signal of DC-DC power converters[J], IEEE trans. on Power Electronics,1996,11(1):132-141 .
[2]蔡宣三，龚绍文. 高频功率电子学. 北京科学出版社 1993年5月.
[3]LEE Y S ,et al. Use of SPICE in design of power electronic circuits and system[A]. IPEMc97[C],Hangzhou,China,717~721 .
[4]张占松，蔡宣三.　开关电源的原理与设计. 电子工业出版社2001年 3月.
[5]陈艳峰, 丘水生.　PWM开关功率变换器分析与仿真方法简述.　电机与控制学报　 Vol.3　No.3.
[6]刑岩，蔡宣三. 开关型电压调节系统数字仿真的一种新算法. 中国通信学报Ｖol.9, No 3,1988 27.
[7]WONG R c, et al. A fast algorithm for the time-domain simulation of switched-mode piecewise-linear systems[A]. PESC 84[c],281~296.
[8]LUCIANO A M, STOLLO A D M.　A fast time-domain algorithm for the simulation of switching power converters[J]. IEEE Trans.on PE, 1990,5(3):363~370.
[9]CHAN H S ,et al . A fast and exact time-domain simulations of switched-mode power regulation[J]. IEEE　Trans, on IE,1992,39(4): 341~350.
[10]林波涛，丘水生. ＤＣ――ＤＣ开关变换器分析方法的述评[Ｊ]. 电路与系统学报，1998，3（3）：65～72.
[11]R.D. Middlebrook and S.Cuk.　A General Unified Approach to Modeling Switching----Converter Power stage,IEEE PESC Record,1976.
[12]D. J. Shortt and F.C. Lee. Extension of the discrete-average models for converter power stage. IEEE PESC Rec,1983 pp.23-~37.
[13]A. P. iectlcciewiecz, D. Tollick. A Unfied　Topological Approach to modeling DC—DC　Converters. IEEE Trans. Power Electionics,1991,6:11~27.
[14]A. R. Brown　and R. D. Middle brook. Sampled-data modeling of switching regulators　IEEE PESC　Rec　1981,p。p。349~369.
[15]CHETTY　P. R.k. Current injected equivalent circuits approach to modeling　of　switching DC—DC converters in contious inductor conduction　mode[J]. IEEE　Trans.On　AES,1981,17(6).
[16]D. J. Shortt and F.C. Lee.　Improved　Switching Converter Model Using Discrete　and　Averaging Techniques.　IEEE PESC’S　83 Record,1983,23~27.
[17] G.W.Wester , R.D.Middlebrook. Low frequency characterization of switched DC-to-DC converters。 IEEE Trans. on Aerospace and Electronic Systems. Vol.9, No 5,1973,pp.376—385.
[18]Y.S.Lee. A systematic and unified approach to modeling switches in switch—mode　power supplies. IEEE Trans. on Industrial Electronic , Vol. 32, No.4,1985,pp.445—448.
[19]VORPERIAN V.　Simplified　analysis of PWM Converters using the model of the PWM switch. Part I&II[J]. IEEE Trans .on AES,1990,26(3):490~505
[20]周嘉农, 曾小平. ＤＣ―ＤＣ开关变换器的建模与分析的动态评述.华南理工大学学报.Vol 28, No 8, 2000 .
[21]P. Krein and J,Bentd man et al.　On the use of averaging for the analysis power electronic systems　 IEEE Trans. On Power Electronics. Vol. 5, No 2,1990,pp.182~190.
[22]丘水生.　非线性网络与系统[Ｍ]．成都：电子科技大学出版社，1990.
[23]QIU S S, FLANOVSKY I M, STROMSMOE K A. An　equivalent small parameter method for strongly nonlinear　system[J]. Proc, 28th　Midwest Symp. on Circuits and Systems, Lonisville,1985,61~64.
[24]胡广莉.　开关ＤＣ―ＤＣ变换器分析方法的发展 [Ｊ]. 华南师范大学学报，1996（3）：67～72.
[25]林波涛,丘水生。一种统一的准谐振开关变换器的等效电路分析法—高频网络平均法[J]. 电子学报,1995,23(8):71-74.
[26]刘健，陈治明，钟彦儒.　多路独立输出的继承谐振DC—DC变换器及其计算机仿真.　微电子学与计算机 Vol.13,No.3,1996,pp.31-34.
[27]林波涛,丘水生.　适于瞬态分析的等效小参量法及其在PWM开关变换器中的应用[J].　电子科学学刊,1997,19(5):649-657.
您打印的此文来自：

作者：王媛彬 … 来源：《电源世界》点击数：

【字体：小大】