 |
【字体:小 大】 |
| 开关电源滑动模型图形分析方法 | |
| http://www.dykf.com 2008/12/10 电源开发网 | |
|
Abstract: This paper proposes a scheme of selecting parameters of the slide mode of switching power supply by phase plane figure. As a boost converter for example, by modeling and simulating it, the result of simulation is identical with the theory analysis and prove that the method is more simple and efficient than the general method! Keyword:slide model, switching power supply, phase plane figure, parameter 1 引 言 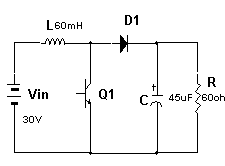 以输出电压 和电感电流 作为状态变量。T表示开关的开关状态,T=1表示开关开通,T=0表示开关关断。当T=1时,其状态方程为: 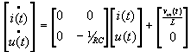 当T=0时,其状态方程为 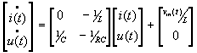 两者合并为 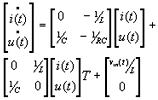 稳态时, 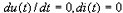 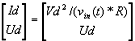 以误差  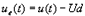 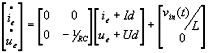 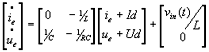 4 相平面图 利用计算机(本文采用MATLAB)分别作出式(5)和(6)的相平面图,设定电源为恒定值30伏,输出电压设定为60伏,L=60mH,C=45μF,R=60Ω。 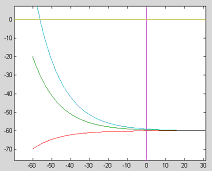  图2是由方程(5)确定的,对实际电路进行定性分析可知,当开关闭合后,由于无能量从电源端向输出端传递,达到稳定时,输出电压渐变为零,那么误差就稳定在-60伏。电源经过电感放电,电流是线性增大的,因此电流误差先减少后增大。这与仿真结果相同。图3将两种状态的相平面画在一起,其中逆时针旋转曲线由方程(6)确定,分析实际电路可知,输出电压最后稳定于30伏,即与输入电压相同,那么误差稳定于-30,仿真结果与分析结果相同。 5 三要素分析及试验仿真 下面我们通过相平面各个区域的运动特性来分析滑模控制的三要素,并通过不同参数的选择来分析参数对系统性能的影响。 从图1我们可以看出,在实际电路中,输出电压不可能等于负值,因此只有电压误差大于等于-60伏的空间对于我们的研究才有意义。 由于开关的频率不可能为无穷大,同时控制电路本身所具有的延时性,从而容易产生抖动,这也是制约滑模控制发展的主要因素。本系统为了减少抖动,采用指数趋近率 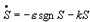 切换面为  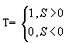 下面我们通过不同的  5.1 切换面为  切换面为  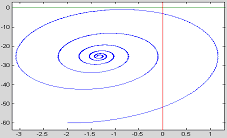  5.2 切换面为  切换面为 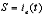 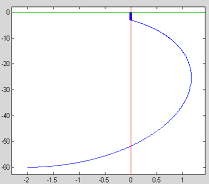 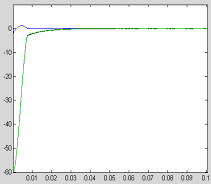 5.3 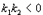 接下来分析切换面在一,三相的情况:如图3,开始于(-2,-60)即初始状态的运动轨迹有两个,一个是当T=1时系统的运动轨迹(直线),另一个是T=0时系统的运动轨迹(逆时针曲线)。要让系统运动进入滑动面 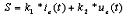   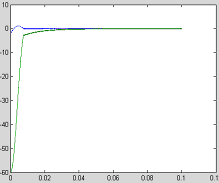 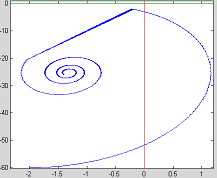  5.4  当切换面位于二,四相限时,在电压误差等于-60伏以上空间,T=1,T=0时系统的运动轨迹在同一过程中都有两次经过切换面,一个是远离切换面,另一个是进入切换面。由文献[3]可知,虽然系统有机会进入切换面,但在切换面上不可能产生滑动运动,所以不适宜在此区域选择切换面。 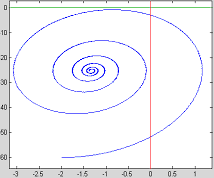 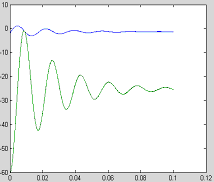 仿真结果完全与分析一致。该方法借助计算机,没有复杂的公式推导,而且比较直观,从而证明该方法正确性和简单性。 6 结 论 本文通过图形法分析开关电源的滑动模型,确定了保证系统稳定的参数的选择范围以及分析了运动特性变化的特点。从仿真结果上证明该方法比传统分析方法简单、直观。但由于作图的维数限制,应此该方法只能应用于三阶及三阶以下系统。而开关电源有很大一部分是二阶,三阶系统,比如说Boost,Buck,正激变换器,反激变换器等都是二阶系统,因此该方法的提出对于滑模控制在开关电源中的研究是很有意义的! 参考文献 1.周宇飞等,Boost变换器滑模控制方法及其实验研究,电力电子技术[J]2000.1.4:42-44 2.朱长海等,基于滑模控制的Buck-Boost型AC-DC变换器,洛阳工学院学报[J]2002.23(1):85-88 3.姚琼荟,黄继起,吴汉松,变结构控制系统,四川:重庆大学出版社,1997:14-52 您打印的此文来自: |
|
| 作者:文锋 袁… 来源:《电源世界》 点击数: |
| - | 【字体:小 大】 |