 |
【字体:小 大】 |
| 次级采用辅助网络的ZVZCS PWM DC/DC 全桥变换器分析与建模 | |
| http://www.dykf.com 2007/2/24 电源开发网 | |
|
次级采用辅助网络的ZVZCS PWM DC/DC 全桥变换器分析与建模 郑颍楠 杨晓波 燕山大学 (秦皇岛 河北大街438号 邮编:066004) 摘 要:分析了一种ZVZCS PWM DC/DC 全桥变换器的工作原理。在此基础上建立了小信号模型,并与Buck电路和ZVS-FB PWM的小信号模型比较,结果表明ZVZCS FB-PWM的小信号模型明显异于后两者。利用小信号模型,设计了补偿网络,给出了仿真结果。 关键词:移相电路 零电压零电流开关 辅助网络 小信号模型 Analysis and Modeling of the ZVZCS Full Bridge PWM DC-DC Converter Using A Secondary Auxiliary Circuit Abstract: A novel ZVZCS FB-PWM DC/DC converter is analyzed in this paper. Comparing with the small signal models of the Buck converter and the ZVS-FB PWM converter, the paper indicates that the ZVZCS small signal properties are significantly different from the latter. On the basis of small signal modeling, the compensation network is designed and verified by the simulation results. Keywords:Phase-shift circuit ZVZCS Auxiliary Circuit Small Signal model 1 引 言 在3kW移相全桥电源模块的设计过程中,考虑到输入电压比较高(三相市电),选用IGBT作为功率开关管。为了增加开关频率,进一步减小电源模块的体积,采用了ZVZCS软开关技术以降低IGBT的功耗。近年来提出了多种ZVZCS FB-PWM 变换器,即利用超前桥臂实现ZVS,滞后桥臂实现ZCS。本文中分析的ZVZCS FB-PWM变换器通过在变压器副边增加由一个小的电容和两个二极管构成辅助电路,实现了ZVZCS,并省去了副边整流器的钳位电路[1]。这种电路具有负载范围宽,占空比丢失小,器件上承受的电压电流应力小,成本低等显著优点,非常适合应用于高功率,高能量密度的电源设计中。主电路拓扑如图1。
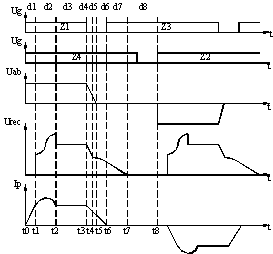
图1 ZVZCS FB-PWM变换器电路拓扑 电路的拓扑可以看成由基本Buck电路衍生,并且与 ZVS FB-PWM电路相似。但是通过下面的分析可以看出,它们的小信号特性有显著不同。这种不同是由其移相特性和引入的辅助电容形成的。本文通过对图1电路的工作过程分析,推导了小信号模型。在相同的电路参数下,与Buck电路和ZVS FB-PWM电路作出了比较,给出了仿真结果。 2 工作原理 图2所示为电路稳态时的工作波形。 为了简化分析,作如下假定: 1)忽略开关管、整流管导通电阻及导通压降; 2)输出滤波电容Co很大,输出电压在整个周期中近似为常数; 3)输出滤波电感Lo很大,滤波电感电流在整个周期中近似为常数。 4)电容Cc的值比较小,副边整流器电压能够在开关导通周期内上升到谐振峰值,电容Cc上的电压在续流阶段下降到零值。
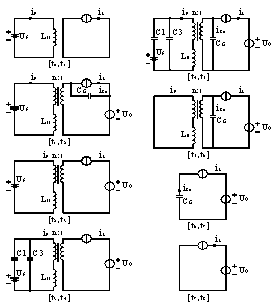
图2 ZVZCS FB-PWM电路稳态工作波形 电路在半个工作周期内可以分为8个工作模式,各个工作模式所占的占空比依次记为d1..d8。 电路在各个工作模式下的等效电路见图3。 在
图3 各个工作模式等效电路 [t0, t1 ]:在这个阶段开始时刻,开关管Z4开始导通,原边电流由0开始逐渐增加。副边整流管Dr1,Dr4电流逐渐增加,Dr2,Dr3电流逐渐减小,直到原边电流增至
其中 [t1, t2 ]:在
其中 [t2, t3 ]:
[t3, t4 ]:开关管Z1关断,原边电流ip近似恒值对C1充电,对C2放电。原边电压线性下降,并且副边电压也以同样的速率下降,直到副边电压下降到等于辅助电容Cc的电压。在这个阶段:
[t4, t5 ]:当副边电压低于钳位电容Cc电压
[t5, t6 ]:原边电压uab降为0,副边的反射电压全部加在漏感上,原边电流迅速下降,到这个阶段结束时刻,原边电流下降为0。在这个阶段:
[t6, t7 ]:原边电流完全复位,整流二极管Dr1,Dr4关断。Cc提供全部的负载电流,Cc上的电压迅速下降为0。在这个阶段:
[t7, t8 ]:Cc上电压降为0,负载电流通过四个整流二极管续流,直到Z2开通,下半个工作周期开始。 3 小信号模型的建立与分析 对输出电感Lo两端的电压在半个周期内积分[3],由伏秒平衡原则,有:
定义
与(3-1)联立,忽略Ceq的影响,解得:
可以看出,ZVZCS FB-PWM电路的有效占空比除了与原边占空比d有关外,还受到输入电压
其中
将上面的分析引入到Buck小信号等效电路模型中[2-4],从而得到ZVZCS FB-PWM变换器的小信号等效电路模型。见图4。
由图4可以进行小信号分析,解得控制对输出传函:
其中: 由ZVZCS的小信号模型,可以观察到由一个内建电流反馈,注意到 在给定的参数条件下,
阻尼系数:
4 仿真结果 在式(3-10)中,如果Rd=0,式(3-10)即为Buck电路的控制对输出传函;由参考文献[4],如果 依据Buck电路,ZVS-FB PWM电路和ZVZCS FB-PWM电路的控制对输出传函可以绘出其波德图,见图5。
采用的数据如下:
从图5中可以看出,Buck电路在固有频率处存在谐振峰值,而ZVS和ZVZCS电路由于内建电流反馈作用,增加了阻尼系数,削弱了谐振峰值。这种现象可以由PSpice仿真进行验证,图6为Buck电路,ZVS电路和ZVZCS电路在PSpice仿真环境下的开环阶跃响应,仿真中采用的数据同上。可以看出,Buck电路的阶跃响应有较大的超调,而ZVS电路和ZVZCS电路,由于其内建电流环的作用,超调量比较小,对于ZVZCS电路尤为明显。
图6-电路拓扑阶跃响应-Buck, ZVS与ZVZCS 5 补偿网络的设计 由以上分析,可以得到ZVZCS在给定参数下的控制对输出传函:
解得特征方程的根:
可以看出,p2>>p1,因此可以将极点p2对系统的影响忽略不计,这样系统就可以用一阶系统来近似:
采用的PI调节器可以表示为:
采用根轨迹设计方法,按二阶工程最佳参计,通过计算得到:
闭环传函单位阶跃响应如图7。 可以看出,在PI调节器的补偿下,系统很容易实现较理想的动态响应特性。
在PSpice仿真环境中对电路拓扑进行的闭环仿真验证了这个结果,见图8。
图8 输入扰动下的输出电压 6 结 论: 本文通过对ZVZCS FB-PWM变换器电路的分析,建立了小信号模型,通过与Buck电路及ZVS FB-PWM电路的小信号模型作比较,可知ZVZCS FB-PWM电路特性与前两者,尤其是Buck电路,有明显不同,不能简单的套用Buck电路的小信号模型。分析了电路参数对输出的影响。利用小信号模型,设计了调节器;由于ZVZCS电路存在内建的电流负反馈,使得系统接近于一阶系统,从而简化了调节器的设计。通过仿真验证了模型的正确。 文中分析的情况是在电容Cc的值比较小,副边整流器电压能够在开关导通周期内上升到谐振峰值,电容Cc上的电压在续流阶段下降到零值的情况下得到的,对于Cc值较大的情况未作分析,需要进一步研究与讨论。 参考文献: [1]: Cho, Jung G., Baek, Ju W., Jeong, Chang Y., Yoo, Dong W., Lee, Hong S., Rim, Geun H. Novel zero voltage and zero current switching (ZVZCS) full bridge PWM converter using a simple auxiliary circuit IEEE Applied Power Electronics Conference and Exposition - APEC v 2 Feb 15-19 1998 [2]: Choi, Hangseok; Kim, J.W.; Lee, J.H.; Cho, B.H. Modeling, analysis and design of 10 kW parallel module zero-voltage zero-current switched full bridge PWM converter. IEEE Applied Power Electronics Conference and Exposition - APEC 1 Feb 06-10 2000 [3]: Vlatkovic, Vlatko; Sabate, Juan A.; Ridley, Raymond B.; Lee, Fred C.; Cho, Bo H. Small-signal analysis of the phase-shifted PWM converter. IEEE Transactions on Power Electronics, v 7 n 1 Jan 1992 p 128-135 [4]: 王艳丹, 蔡宣三. 全桥零电压开关-脉宽调制变换器的小信号分析与最优控制. 清华大学学报(自然科学版). Vol. 34 No. 4 1994 作者简介: 郑颖楠 男,1955年,教授。研究方向为PFC技术和特种电源。 杨晓波 男,1973年,硕士研究生,主要研究方向为模块化电源与均流技术 您打印的此文来自: |
|
| 作者:郑颍楠 杨… 来源:电源技术应用 点击数: |
| - | 【字体:小 大】 |

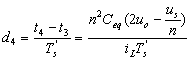 (2-4b)
(2-4b) (2-5b)
(2-5b)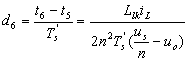 (2-6b)
(2-6b) (2-7b)
(2-7b) (3-1)
(3-1) (3-3)
(3-3)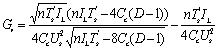 (3-5)
(3-5) 图4 ZVZCS FB-PWM电路小信号模型
图4 ZVZCS FB-PWM电路小信号模型  (3-7)
(3-7) (3-10)
(3-10) 图5 控制对输出传函-Buck,ZVS与ZVZCS
图5 控制对输出传函-Buck,ZVS与ZVZCS 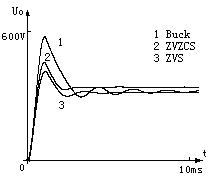
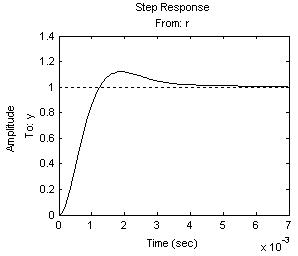 图7 系统闭环单位阶跃响应
图7 系统闭环单位阶跃响应 