|
【字体:小 大】 |
| 开关电源功率因数校正的DSP实现 | |
| http://www.dykf.com 2007/7/21 电源开发网 | |
|
开关电源功率因数校正的DSP实现 厉冰,林国淑 (西安交通大学电子物理所,陕西 西安 710049) Abstract:A DSP based solution for power factor correction of switching power supply is introduced.The principle, algorithm and detailed implementation are discussed . At last, experiment results are provided. Keywords:DSP; Power factor correction(PFC); Switching power supply 1 引言 随着对高功率因数的变换器的需求不断增长,功率因数为1(unity power factor)的电源供给越来越受到欢迎。在计算机或其它一些设备上,电源要求鲁棒性好、可靠、抗干扰能力强。而数字控制正提供了这方面的保障。 和传统模拟控制器相比,数字控制器具有以下这些优点:可以实现非线性的精细的控制算法,减少元器件数量,提高可靠性,不易老化,很小的控制偏差和热漂移。但同时,数字控制也意味着相对较高的费用和一定的控制带宽限制。过去,这些不足在很大程度上限制了数字控制在电源方面的应用。而现在,由于高效廉价的DSP的出现,数字控制不仅在交流驱动(ACdrives)和三相变换方面应用越来越广泛,而且在DC/DC变换领域也成为一种可行方案。本文将讨论DSP在单相开关电源功率因数校正方面的应用。 2 传统的模拟PFC电路简介 模拟PFC电路已经有了多年的应用,并且推出了一些商用的IC芯片,例如TI公司的UC3854等。 图1所示的就是功率因数校正的基本原理。PFC控制电路主要由电压误差放大器、电流误差放大器、乘法器和PWM驱动组成。控制的目标是使输入电流紧跟输入电压的变化,并使输出纹波尽可能地小。为了使输入电流跟随输入电压变化,控制电路对输入电压采样,采样信号作为乘法器的一个输入;为了保持输入电压稳定,输出电压经分压、比较和误差放大后作为乘法器的另一个输入,于是乘法器的输出具有输入电压的形状,且其幅度由输出电压控制。乘法器的输出作为输入电流的基准信号。采样输入电流,和这个基准比较,经误差放大后输入PWM比较器,PWM输出驱动波形控制变换器工作。闭环反馈控制的结果使输入电流的平均值与输入电压成正比,从而达到较高的功率因数。
图1 功率因数校正原理 PFC变换器的输出中含有二次谐波的纹波电压, |ΔVo(t)|= 这与变换器的拓扑结构和控制方式无关。如果要通过电压回路消除输出电压的纹波,就必然会损坏输入电流的波形,从而降低功率因数。而引入模拟滤波电路 的话,又会引入不良的相位影响,而且由于模拟元件参数离散性大、易老化和热漂移等因素,很难实现精确的滤波。所以对于50Hz的工频输入,电压回路的带宽一般都只选在10~20Hz。 3 数字控制的PFC模型 如图2所示是Boost电路PFC的数字化模型。该模型的控制原理与前面所述的模拟电路是一致的。区别就是用两个数字的比例积分控制器(PI)Ki、Kv代替了原来的两个误差放大器。另外,在电压PI的输出端加了一个陷波滤波器,滤波频率为100Hz。与模拟滤波器相比,数字滤波可以很好地减少100Hz的谐波成分,同时引入的相位影响却要小得多。
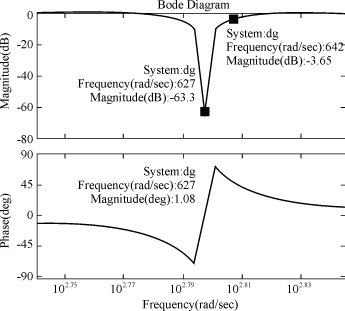
图2 数字控制的PFC模型 这样,就可以提高电压回路的带宽,继而提高电路的反应速度。 如图2所示,三个信号被采样,分别是输出电压Vo,输入电流Is,输入电压Vi′。其中值得注意的一点是,我们可以编程实现总是在开关闭合的中间时间对Is采样,从而不需要另加低通滤波就可以获得Is的平均值。 接下来我们分别建立PI控制器和陷波滤波器的数字模型。PI控制算法的模拟表达式为 V(t)=Kp 对式(2)进行离散化处理,得到 V(n)=Kp[e(n)-e(n-1)]+Ki·e(n)+V(n-1) (3) 式中:Kp为比例系数; Ki= PI系数的整定常常通过实验来确定,或通过凑试,或者通过经验公式来确定。这方面的内容一般的计算机控制系统类的书上都有介绍。 陷波滤波器的设计可参照公式(4) 式中:ω是滤波频率的角速度; Q值按不同的要求确定。 离散化可以由Matlab的sysd=c2d(sys,Ts)方程方便地实现。图3所示的就是所设计滤波器的Matlab模拟图,其中ω=628,Q=20。
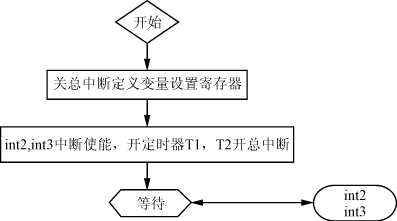
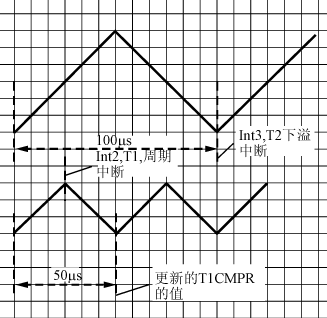
图3 数字陷波器的Matlab模拟 4 DSP实现 我们采用TI公司的16位芯片TMS320LF2407A来实施控制方案。这款芯片专门用于数字控制的2000系列,采用哈佛结构的CPU和4级流水性操作的程序控制,运行速度是40MIPS(即25ns的指令周期)。它具有544字节的DARAM,2k的SARAM,32k的FLASH,2个事件管理单元,16路10bit、转换时间500ns的A/D转换,最多16路的PWM输出等片内资源。 对电流回路和电压回路,我们分别采取20kHz和10kHz的控制频率。两个中断程序被用来完成PFC的数字控制,中断程序int2负责3个输入的采样及电流回路的PI控制,另一个中断程序int3负责电压回路的PI控制及陷波滤波。图4是主程序控制流程图,图5是采样周期图。其中int2的中断优先级高于int3,所以若int3没完成,而int2中断发生时,int3将悬挂直到int2中断程序运行结束才继续运行。因为电压回路的变化比较缓慢,所以一个周期的延时不会影响控制效果。设置比较控制寄存器,在T1下溢的时候写入新的比较值,结合通用定时器周期寄存器T1PR的值,产生新的占空比的PWM波,控制与之相连的开关管的动作。从图5中我们也可以注意到,int2的中断程序(包括3个采样和一个PI程序)必须在半个电流采样周期,即25μs之内完成。根据前面给出的DSP的性能指标,这个目标完全可以达到。
图4 主程序流程图
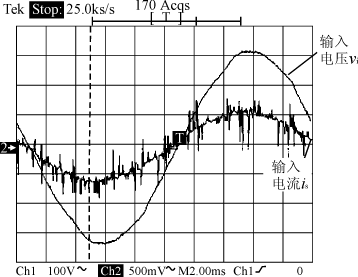
图5 采样周期图 另外,在实际应用中,采用的是积分分离的PI算法,把PI的输出值限定在一定的范围之内,避免使系统产生很大的超调量而引起系统振荡。还加入了软启动程序,在程序刚开始的时候逐步加大Vref的值,从而达到开关电源的软启动要求。 因为像Kp,Ki及滤波器系数等这些参数都是浮点数,而所用的是16位的芯片,所以用DSP实现以上算法,还需要解决浮点数和定点数之间相互转换的问题。可以用不同的Qn值来表达不同范围和精度的浮点数,其中n表示16位中小数点之后的位数。例如,Q0可表示-32768到32767的整数,而Q15可表达-1到0.9999695之间精度为1/32768的实数[2]。不同的Qn值之间需要经过移位,转换为相同的位数才能进行比较和加减运算。 5 实验结果 程序编译通过后,烧入片内flash,外加简单的外围电路,就可以进行实验验证了。我们采用的是Boost电路的拓扑结构,接电阻负载,输入电压220V,输出电压385V,得到的输入电压电流波形如图6所示。用功率表测得PFC电路的输入功率为545W,输出功率为513W,可以计算出PFC电路变换效率为94.1%。在相同测试条件下,用功率因数表测得的PFC电路的功率因数为0.983。图7所示的是软启过程。
图6 BOOSTPFC电路输入电压电流图
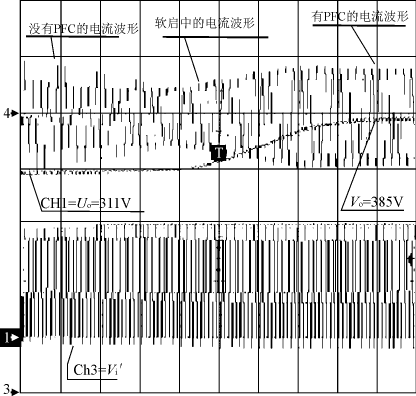
图7 软启动波形图 6 结语 本文探讨了开关电源功率因数调整的全数字实现方案,实验证明了该方案的可行性。目前,对开关整流器件采用DSP控制的研究开展的还不多,主要是由于相对于专用的集成芯片DSP的价格比较高昂,而且成熟的控制算法难以获得。然而,随着DSP芯片价格的不断降低和控制算法的研究不断深入,相信开关整流器件数字控制的时代很快就会到来。 参考文献 [1]S.Buso,P.Mattavelli,L.Rossetto,G.Spiazzi, Simple digital control improving dynamic performance of power factor preregulators[J].IEEE TRANSACTIONS ON POWER ELECTRONICS (13)5,1998. [2] U- 134,UC3854 Controlled Power factor Correction Circuit Design, Power Supply Control Products Data Book[M].Texas Instruments. [3] TMS320LF/LC240XA DSP Controllers Reference Guide Tech.Rep. SPRU357B ,Texas Instruments,2001. 您打印的此文来自: |
|
| 作者:厉冰 林国… 来源:电源技术应用0301 点击数: |
| - | 【字体:小 大】 |