|
【字体:小 大】 |
| 临界模式下的单级功率因数校正电路及储能电容电压控制的研究 | |
| http://www.dykf.com 2007/2/24 电源开发网 | |
|
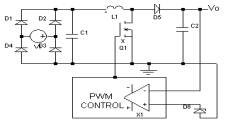
临界模式下的单级功率因数校正电路及储能电容电压控制的研究 邓卫华 张 波 (华南理工大学, 广东 广州 510640) 摘 要:本文首次分析了单级功率因数校正(PFC)电路中的电流畸变特性,得出PFC电路的功率因数及其总谐波畸变的解析表达式。在此基础上,本文首次提出了一种全新的临界工作模式下的单级功率因数校正电路,在对PFC变换器及DC/DC变换器工作在连续及不连续的边界条件进行了讨论后,得出了电路工作状态的精确解并提出了控制储能电容电压的临界点工作方式。该电路在利用普通控制芯片实现较高功率因数的同时,有效地控制了储能电容的电压值,降低了开关应力,提高了电路的效率。实验验证了本文数学推导的正确性和控制策略的实用性。 关键词:连续工作模式 不连续工作模式 功率因数校正 中图分类号:TM46 文献标示码: Analysis of working mode of converter and voltage control of buck capacitor in single-stage Power Factor Correctors DENG Wei-hua,ZHANG Bo ( South China University of Technology, Guangzhou 510640) Abstract: Analysis of power factor and line current harmonic of single-stage Active Power Factor Corrector is presented firstly. Then the paper presents a novel-working mode of Boost-Forward single-stage Power Factor Correctors based on the analysis. And get the principle of the conduction mode and the method to control the voltage of the buck capacitor after the analysis of the boundary mode of the PFC converter and the DC-DC converter. The circuit uses a common IC to realize the high PF and decrease the voltage of the capacitor and increase the efficiency. The circuit performance was verified experimentally. Key words: Continuous Conduction Mode (CCM) Discontinuous Conduction Mode (DCM) Power Factor Correction (PFC) 1 引 言 功率因数校正技术的发展呈现两级发展的趋势,其一是应用在大功率高精度电源上的双级功率因数校正技术,该方法采用专用PFC控制芯片,控制性能好,但成本高,一般的中小功率电源难以接受;其二是应用在中小功率电源中利用电压自动跟随技术的功率因数校正电路即不连续工作模式(DCM)功率因数校正电路[1]。在DCM模式下,通过适当的设计使得输入电流自动跟随输入电压的变化实现功率因数补偿,该类电路有控制简单,成本低廉和便于应用的特点。近年来提出的单级组合PFC电路更加表现出其优越性。 但至今对于PFC变换器有三方面问题的研究还不够深入,即输入电流畸变,变换器的临界条件以及稳态特性的研究。尤其是采用单级结构后,由于PFC和DC-DC变换器存在着不可避免的联系,当输入电压达到最大值且负载最轻时,储能电容上的电压会大幅增加,电路稳定性受到很大的影响。因而控制储能电容电压是该类电路要解决的重要问题之一。 对此,本文将结合DCM模式下的单级PFC变换器进行严格的数学推理,深入地研究了PFC电路的输入电流畸变问题,得出电流畸变的数学解析式。然后,本文针对Boost-Forward单级功率因数校正电路,在对PFC电路及DC/DC电路工作在连续及不连续的边界条件进行了讨论后,得出了电路工作状态转换的精确解。 在此基础上本文提出了临界工作模式,即通过电路的负载范围设计变换器,让电路工作在电感临界点并随负载变化自动调节电路工作方式,即可保持高功率因数的同时控制了储能电容电压值,让电路的稳态特性得到较好的保证。 2 电流波形的畸变分析 2.1 输入电流解析式 首先分析PFC变换器的输入电流畸变。在单级DCM模式PFC电路中,通过电压跟随方式取得的电流波形并非纯粹的正弦波,对于输入电流在固定占空比下被分解为三角脉冲波,电感电流峰值将自动跟随正弦输入电压。但是,由于输入电感电流放电时间的调制,输入电流的平均值不会与输入电压成正比,因而输入电流会呈现一定程度的畸变,并随电感电流的放电时间的变化而产生畸变。 电压跟随型功率因数校正电路原理如图1所示。电路常采用Boost结构作为PFC变换器,当Boost电感工作在不连续模态时,开关的控制占空比由boost输出滤波电容的输出电压或后级DC/DC变换器的输出电压的反馈值控制。由于Boost电感电流峰值Ib=Vin.Ton/Lb决定,而输入电压Vin是正弦变化量,因而电流峰值Ib将会自动跟随输入电压波形[2]。
图1 电压跟随型功率因数校正电路 在电压跟随型功率因数校正电路中,开关频率一定时,占空比在一个工频周期内基本上处于恒定,假设输入电压为
式中T为开关周期,D为占空比,电感电流将会跟随输入电压包络线。 当开关关断时,电感电流开始放电,并承受反向电压Vo-Vin,Vo为Boost电路输出电压,可得放电时间为[2]:
由式(2)可得放电平均电流
则输入电流表达为: 由公式(6)可知,当α非常小时,输入电流接近正弦,当α接近1时,输入电流畸变就会很严重。图2所示为波形与α的关系图。
2.2 功率因数表达式 功率因数被定义为实际输入有功Pin比上输入的视在功率[1],即:
其中:
式(8)中定义 式(7)中
其(10)中定义
现对式(9)和式(11)进行积分解析直接计算结果[3][4]:
(9) 式和 (11) 式也可由数字解法解出结果。最后化简可得功率因数表达式[3]:
图3所示为功率因数随α变化关系,由图可见,当小于0.8时,功率因数高于0.95,功率因数会随α增大而减小,当α大于0.9时功率因数会迅速减小。
通过分析得知,波形畸变是有关输入电压峰值和输出电压的函数。通常可以认为变换器的输入电压恒定,即储能电容的电压很大程度上决定了功率因数的大小,下面将要重点分析储能电容电压值的变化。 3 单级PFC电路的临界工作模式 3.1 PFC电路临界模态的定义 图4所示为一典型的单级PFC电路,其拓扑结构为Boost-Forward电路。图中,电感Lb为升压电感,Lf为输出滤波电感,开关S将功率因数校正级和电压变换级合成一级。储能电容Ce即作为PFC电路的输出端又作为DC-DC变换器的输入端。 对于Boost变换器,在一个工频周期内,开关S的占空比是基本上恒定不变的,因而PFC级即可在DCM下工作也可在CCM下工作。若工作在DCM模式,输入电流自然跟随输入电压,可获得接近1的输入功率因数[1]。占空比由输出电压误差信号控制来实现输出电压的快速调节。对于PFC电路工作在CCM时,输入电流的电压跟随特性不如DCM模式好,而且采用常规的脉冲宽度调节来控制输出电压时,储能电容电压随负载变化较大,难以控制,但如果PFC电路在一般负载下工作在DCM模态,在重载下工作在CCM模态,可以减小开关承受的电流峰值以及减小导通损耗及其EMI,而且功率因数不会降低太多。因此可采用DCM模式进入CCM模式的工作方式。
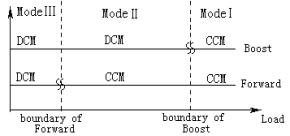
图4 单级单开关Boost-Forward电路 Forward变换器输入电压为储能电容器Ce两端电压Vce,其稳态值与电感Lf的工作方式有关。为了提高变换器的效率,Forward变换器一般采用电流连续模式工作(CCM)。当Lf工作在CCM时,Vce与占空比无关,当负载变轻时,输出功率变小,占空比不随负载变化而变化。这样充入储能电容的功率大于从储能电容中抽走的功率,导致储能电压的升高。为了保持输出电压的稳定,电压反馈环调节占空比减小,从而相应地减小输入功率,这个过程直到电容输入输出功率达到平衡为止。 而当Lf工作在DCM时Vce随占空比D的增大而增大;输出电压则随占空比D的增大而增大,此时电容两端的电压Vce较Lf工作在CCM时的值低。因此可选定变换器在输出电流较低时,让Lf进入临界点,转换为DCM模式,从而能够有效地抑止电容器Ce两端的电压,降低开关器件的电压应力,从而保证变换器的稳态工作特性。 变换器临界点及工作模态随负载变化如图5所示。 在定义了单级PFC电路的临界工作模式后,就需要确定Boost变换器和Forward变换器的临界条件,然后通过选择变换器的参数使得变换器工作在所要求的临界工作模式下。
图5 变换器工作模式图变化图 3.2 Boost变换器工作模态分析 首先分析PFC电路中的Boost变换器的工作特性并确定其临界点。图6所示的为图4中Boost-Forward电路的去耦等效电路。
图6 Boost-Forward去耦等效电路 可以看出,该电路在n=1,Lb=0时即为Boost-Buck电路。图中的参数对应关系为[1][2]:
由图5可见,Lb,L1,S,Ce,D构成Boost变换器,变换器在一个开关周期内平均输入功率为: 由文献[1],当电感Lb处于临界条件时,有
假设变换器的效率为η,由式(16)(17)则可得到Boost电感的临界条件为:
当K1>KCRIT,1时,Lb工作在CCM,当K1<KCRIT,1时,Lb工作在DCM。 3.3 Forward工作模态分析 对于DC-DC变换器,本文选用Forward变换器。假设Lf工作在CCM状态与DCM状态的临界点,则变换器存在两个工作状态,每个开关周期流过Lf的平均电流为:
同时考虑到: 在电感Lf处于临界条件时,Vo,r和Vce之间满足Vo,r=DVce,即可得出电感Lf工作在DCM和CCM的临界条件为:
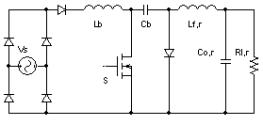
也即当K2>KCRIT,2时,L2工作在CCM,当K2<KCRIT,2时,L2工作在DCM。 4 实验电路设计及实验结果 根据上述理论分析以及设计原则研制了一台临界点工作方式的单级Boost-Forward功率因数校正电路,其中Forward电路采用了变压器不易饱和,同时驱动简单的双管正激变换器。电路采用图7所示电路,变换器采用临界点工作方式,即当电路负载很轻时Boost电感工作在DCM模态以确保高功率因数,后级Forward电路工作在DCM防止储能电容电压过高,然后随输出电流增大,Forward电路进入CCM工作模态以确保电路的高的传输效率,当输出负载较重时可以让Boost变换器进入CCM模式,从而减小了在整个负载范围内Boost变换器的峰值电流应力并较小了开关的导通损耗,同时功率因数保持在较高值。整个电路在确保较高功率因数同时提高了效率,并限止了储能电容及开关器件的电压应力。
实验电路图设计参数为:Vin=110~240V,Vo=12V,Po=100W,变压器Lp=2.32mH,Ls=137uH,Ce=270uH,Co=2200Uh,fs=150KHz,D=20%。按照上述分析,我们选取负载变化使得Boost电路工作在DCM模式,然后改变负载,让Forward电路工作在临界点。一般负载工作在1Ω~30Ω,当负载RL>28Ω,Io<0.5A时输出电流减小,同时储能电容电压升高,可让Forward电感电流进入不连续导电模式,确定Lf工作临界点;当电路负载进入满载时RL<2.5Ω,可让Boost电感进入CCM模式,确定Lb工作临界点。按照上述分析,我们选取输出电感值使得其工作状态为临界点,由公式(18)(19)及(22)(23)代入数据可求得Lb=80uH,Lf=70uH。电容电压变化曲线如图8所示,Forward电感电流如图9所示。
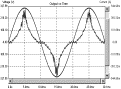
(a) CCM模式Io=3A (b) 临界点模式Io=0.5A (c) DCM模式 Io=0.1A 图9 Forward电感Lf=70uH时电流波形图 当Lb=80uH时负载RL<2.5Ω,Io>5A时,Boost电感进入连续导电模式,虽然此时功率因数不如DCM时高,但仍然能保证满足各项谐波标准的要求,功率因数变化如图10所示,Boost电感电流如图11所示,左图为一个工频周期内的电感电流波形,右图为开关周期内的电感电流波形。
(a) DCM模式 Io=2A
(b)临界点模式Io=5A
(c)CCM模式Io=6A 图11 Lb=80uH时Boost电感电流图 电路的功率因数及谐波成分的测量[5]采用的是基于HP I/O 库建立的虚拟仪器测试平台。该测试平台采用IEEE-488 GPIB标准,测量仪器通过数据采集卡将测量的数据传给计算机,然后由控制软件进行分析处理,得到详细而精确的测量结果。功率因数采用HP交流电源分析仪图形界面(HP Ac Source GUI)测量;谐波分布采用HP 谐波及闪烁测试系统(Harmonic Flicker Test System)测量。由第2节分析可知功率因数只与PFC变换器输入电压及输出电压有关,因此通过调整负载使得PFC变换器及其Forward变换器的工作模态变化,便可控制输出电压,即控制功率因数的大小。
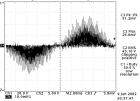
(a) α=0.7,PF=0.974,THD=26%
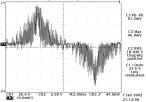
(b) α=0.8,PF=0.93,THD=33%
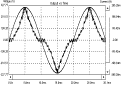
(c) α=0.9,PF=0.90,THD=42% 图12 输入电压电流波形及电流谐波分布图 图12为α=0.7, 0.8, 0.9值时的输入电压电流波形图及电流谐波分布图。当改变负载程度就可改变输入电压值,使得α值改变。可以看出α越大,电流波形畸变就会越大。采用上述电路功率因数最高可达0.97,重载时功率因数偏低,但任能很好的满足IEC1000-3-2标准。图13为设计的 电路实物图。 理论上讲,由于Boost电感电流放电时间的不同,因而输入电流含有一定程度的畸变,从而功率因数也就不会接近1,放电时间越长,则电流畸变就会越大,功率因数就会越低,其表现出来的输出电容电压也就越低。因而在通常输出功率增大的情况下,电感的电流峰值就会增大,电流放电时间就会增长,导致电流高次谐波增大,则表现出来的功率因数就变低了。
图13 电路外形图 5 结 论 采用单级电压跟随型不连续功率因数校正电路为中小功率开关电源提供了一个廉价简便的控制方法,本文针对该类PFC变换器进行了系统的研究从而获得有关单级DCM模式PFC电路的电流谐波的严格解析式以及电路工作模态的临界点。理论分析表明:电路功率因数只与PFC变换器输入电压及输出电压有关,因此通过调整PFC变换器输出电压便可控制功率因数大小,而输出电压和PFC变换器、DC-DC变换器的工作状态以及负载大小有着密切的联系。通过负载情况,设计变换器工作在不同的状态,达到较高的功率因数,较低的储能电容电压,以及较小的电压电流应力从而使得电路的整体工作特性得到较大的提高。本文最后通过一系列试验验证了理论分析的正确性,也为该类电路的实际设计提供了重要理论指导的依据。 参考文献: [1] 严百平,刘建. 不连续导电模式高功率因数开关电源北京.科学出版社.2000 [2] 蔡宣三,龚绍文.高频功率电子学——直流-直流部分.北京.科学出版社.1993 [3] K.S.Fung. Analysis and measurement of DCM Power Factor Correctors. IEEE APEC’99 Conf. Pp.709 [4] M.K.Nalbant. Power Factor Calculation and Measurements. IEEE APEC’90 Conf. Pp.543 [5] 邓卫华,胡宗波,张波. 基于HP I/O库的虚拟仪器与实验平台,仪器仪表学报,2001. 4增刊 您打印的此文来自: |
|
| 作者:邓卫华 张… 来源:电源技术应用 点击数: |
| - | 【字体:小 大】 |
 (5)
(5) 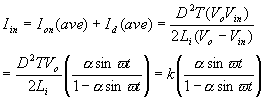 其中,
其中,  图2 输入电流波形与α的关系
图2 输入电流波形与α的关系  (8)
(8) 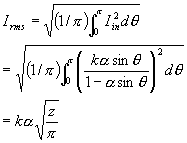 (10)
(10) 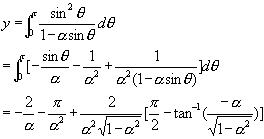 (12)
(12)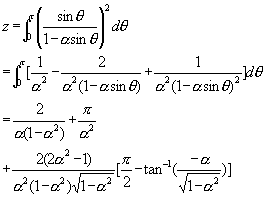 (13)
(13) 图3 功率因数与α关系图
图3 功率因数与α关系图 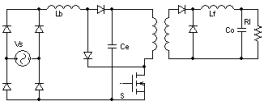
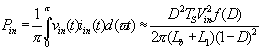 (16) 其中,
(16) 其中, 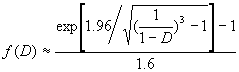
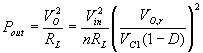 ( 17)
( 17)  图7 Boost-Forward 单级PFC电路
图7 Boost-Forward 单级PFC电路  图8 电容电压变化曲线图
图8 电容电压变化曲线图 


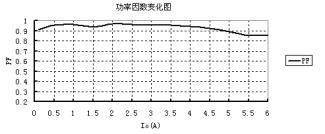 图10 功率因数变化图
图10 功率因数变化图