|
【字体:小 大】 |
| 级联型逆变器相移PWM的相移量与输出谐波关系分析 | |
| http://www.dykf.com 2007/11/5 电源开发网 | |
|
级联型逆变器相移PWM的相移量与输出谐波关系分析 单庆晓,黄元林,陈长明 (国防科技大学机电工程与仪器系,湖南 长沙 410073) 1 引言 多电平逆变器由于可降低器件的开关应力,优化输出波形,提高转换效率等优点,目前在中大功率场合得到越来越广泛的应用。多电平逆变器目前主要包括二极管嵌位型、电容嵌位型、多单元级联型等[1]。级联型逆变器将多个逆变单元串联起来,易于扩展,主要缺点是每个单元需要隔离的直流电源。为减少隔离电源数量,单元电路结构可以不完全相同。这种由不同单元串联而成的逆变器称为混联型逆变器。当电源电压不同时,可以增加输出电平种类[2]。串联单元本身还可以是一个多电平逆变器,如二极管嵌位型逆变器[3]。图1是一个由H逆变桥和五电平逆变器串联组成的混联型逆变器。级联型又可分为带隔离直流电源和带隔离输出变压器2种。分别如图2和图3所示。
图1 混联型逆变器示例
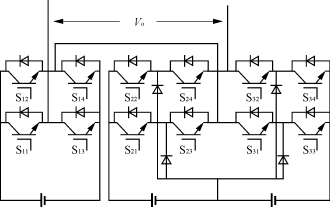
图2 带隔离直流电源的多重结构
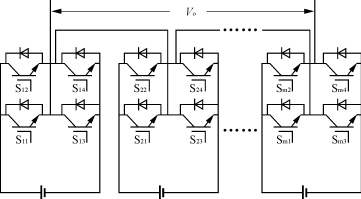
图3 带有输出隔离变压器的多重结构 多电平逆变器输出正弦波的调制方法主要有2种,一种是基于基频的调制方法,使逆变器输出阶梯波逼近正弦波,可分为空间矢量控制和谐波选择消除,通过合适的选择阶梯波的时间和幅度,可有选择地减少或消除特定的开关谐波;另一种是基于高频的调制方法,通过高频调制,使得谐波频率更高,更易于滤除,可分为空间矢量调制和SPWM2种方式。 多电平逆变器中随着级数的增加,空间矢量的个数呈几何次数增加,而数量较多的矢量可获得更好的控制效果。SPWM很易于从两电平方式扩展到多电平方式。多电平SPWM主要有多载波SPWM、相移SPWM和注入3次谐波提高母线电压利用率法。多载波SPWM将多个相邻三角波与正 弦参考信号进行比较得到控制脉冲,适用于二极管嵌位和级联型逆变器。相移SPWM技术适用于级联型逆变器[4][5][6],通过将相位不同的载波信号与正弦参考信号比较得到触发脉冲。图4显示了一个三重级联型逆变器相移SPWM产生原理。相移SPWM可以提高输出波形中含有的谐波频率,从而使之更易于滤除。本文分析了各单体逆变器之间的相移与输出频谱之间的关系,并通过仿真和实验验证了分析结果。
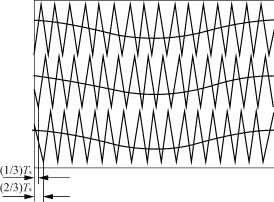
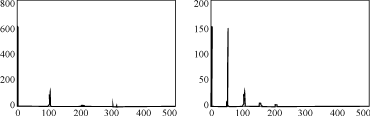
图4 三重级联型逆变器相移SPWM产生原理图 2 相移量与输出频谱之间的关系 对于单体逆变器,其驱动信号产生原理与两电平SPWM逆变器完全相同。而对于不同的单体逆变器,输出的基波存在一个相位差。 设逆变器由m个单体SPWM逆变器组成,第i个SPWM逆变器输出电压为ui,则串联输出总电压为 u0= 设单个逆变器输出单相双极性SPWM波,且波形正负半周期镜像对称,即 u(ωt)=-u(ωt+π)(2) 为简化计算,设波形在正负周期内前后1/4周期以π/2为轴线对称,即 u(ωt)=u(π-ωt)(3) 则可用傅立叶级数表示为[7] u(ωt)= 设逆变器的一个开关周期为Ts,各个逆变器输出时延为Ts/m,则输出电压用傅立叶级数表示为 u(ωt)= 由于 =sinnωt =sinnωt 式中:T为逆变器输出波形基波的周期,当基波为工频50Hz,T=20ms; Ts为开关周期,当开关频率fs为几十至几百kHz,Ts为几μs至几十μs。 当n=1时,可近似认为 可见,串联后输出电压中基频成分为线性叠加。 当n=m 可见,串联后输出电压中频率f=mfs的成分线性叠加。 因此,我们可以得知,m个输出依次时延Ts/m的SPWM逆变器串联,其输出的基频成分幅值为线性叠加,输出含有f=amfs(a=1,2,...)的谐波,谐波的幅值亦为线性叠加。 因此,若多重逆变器由m个单体逆变器组成,逆变器载波频率为fs,则第i个单体逆变器的时延为: t= 可见,通过串联叠加,输出频谱中所含谐波成分更加高频化,可大大减小滤波电感的体积。 3 仿真与实验 3.1 基于MATLAB的仿真实验 采用MATLAB对两个时延为Ts/2的单相SPWM叠加得到双重SPWM波的情况进行仿真,条件为:开关频率fs=2.5kHz,调制比为0.8,时延Ts/2。频域分析结果如图5所示。
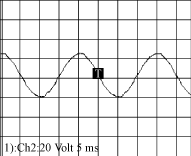
(a) 双重叠加输出电压的频谱分布 (b) 单个逆变器输出电压的频谱分布 图5 不同方式下输出电压的频谱分布 可见叠加后的波形中开关谐波频率增加1倍,基频和谐波成份都得到叠加,证实了以上分析结果。 3.2 电路实验 采用CM15-12H型的IGBT建立带高频输出变压器的单体全桥逆变器,逆变器为二重串联叠加结构,带小型滤波电感。控制方式采用相移PWM控制,采用ADSP2181为数字控制器,输出两路相互有时延的SPWM控制信号。输入电源由4节12V蓄电池串联提供,输出为220V,50Hz交流。 当开关频率为12kHz,时延为τ=42μs,负载为纯阻性,滤波输出波形如图6所示。波形的THD<3%。
图6 实验的输出波形 4 结语 本文对相移PWM的输出频谱进行了分析,得出了时延与输出频谱之间的关系。仿真与实验的结果证实了分析的正确性。 您打印的此文来自: |
|
| 作者:单庆晓 黄… 来源:电源技术应用0308 点击数: |
| - | 【字体:小 大】 |