|
【字体:小 大】 |
| 基于瞬时无功理论电压不平衡三相变流器控制研究 | ||||||||||||||
| http://www.dykf.com 2007/3/2 电源开发网 | ||||||||||||||
|
基于瞬时无功理论电压不平衡三相变流器控制研究 孙孝峰 邬伟扬 (燕山大学 河北 秦皇岛 066004) 摘 要:本文介绍了三相变流器在非平衡状态下,应用瞬时无功功率理论,采用正负序分量分离法来实现对PWM三相变流器进行功率因数校正,采用这种方法,可以有效控制系统的无功,消除谐波,控制效果好 关键词:DQ变换 不对称电压 瞬时无功功率 1 简 介 消除电网谐波是电工技术领域的重大课题。世界上许多国家都制定限制谐波的国家标准或规定。我国也于1984年和1993年分别制定了限制谐波的规定SD126-84和国家标准GB/T14549-93。据美国对全美开关电源市场的调查报告表明,近几年AC/DC 开关电源的需求平均年增长率为12.7%,如果多采用半控或不空整流技术,电网供电质量将急剧恶化。因而基于脉宽调制功率变换电路日益成为人们提高供电系统功率因数,降低谐波污染的有力工具,成为人们研究的热点。三相全控型电压源功率变换装置,主电路如图1所示,经过十余年的研究,已经开始实用化。在对称三相系统中,应用PWM技术,可以有效消除系统的谐波污染,并实现基波的功率因数为1。
然而,目前大多数关于三相功率变换器的研究基于理想工况的,如三相平衡系统。实际生产过程中,由于不间断电源、独立的能量再生设备和以及随机启动的民用用电设备的广泛存在,很难保证供电系统的三相平衡。因此必须考虑在三相不平衡工况下,系统的无功消除问题。对于高频功率变换系统来说,建立在平均值基础上的传统功率理论已经难以适用。80年代初,日本学者赤木泰文 (H. Akagi)等人提出了建立在瞬时值基础上的三相电路瞬时无功功率理论,国内外的许多学者对此问题进行了深入的探讨[1~ 5 ],并成功地应用于实际分析三相电路瞬时无功功率理论与传统功率理论的关系,建立二者的统一数学描述,揭示瞬时无功率的物理意义。这种分析和统一数学描述是基于将传统功率理论中有效值、相位差、有功功率和无功功率等概念向瞬时值概念的自然扩展, 在三相电路中,无功不仅在电源与负载间流动,而且在三相电路之间流动。瞬态时,当三相电路电源与负载间及各相之间有无功流动时,会增加三相电路的总传输损失,同时造成电网的谐波畸变。因此,当我们在进行功率因数校正时,应根据三相瞬时无功理论来进行系统控制。本文应用该理论技术,提出消除平均及瞬态无功的新型单位功率因数控制策略。 2 三相系统无功分析 设三相电路的瞬时电压和瞬时电流分别为
当电压和电流均为正弦对称时,瞬时实功率和瞬时虚功率正好等于传统功率理论中三相电路有功功率和无功功率。当三相电压为正弦对称时,瞬时实功率和虚功率中的直流成分分别与三相电流中基波的有功分量和无功分量对应,而交流成分与三相电流中的谐波分量对应;特别是在一些典型情况下,如当电流为不对称的正弦时,其负序分量转化为p和q中的二次谐波。现在我们在旋转坐标系下,结合三相PWM AC/DC变换电路,具体考虑系统功率与电压、电流动关系。 三相不对称分量可以分解为正序分量、负序分量、零序分量。在三相三线制电路中我们可以忽略零序电压分量的影响。那么,电网电压,输入三相电流,变流器端电压可以表示为:
其中
在旋转坐标系下,各分量在可以表示为
三相变流器的电流电压约束关系为
旋转坐标系下,系统的数学模型可以表示为[4]
系统的示在功率表达式为
根据表达式:
那么,根据文献[4]有功、无功功率达表达式为:
那么,如果以消除系统无功,控制系统平均有功为原则,应有
则,系统期望电流表达式为
根据
其中
3 系统控制方案 我们给出系统的各电流分量的期望值。而在实际系统中,正负序分量同时存在与主电路中,因此必须清楚两者之间是否单独可控。根据式(11)、(3)~(5),我们能够得到稳态时,有:
因此,从上面推导结果可以看出正序电流只与正序电压有关系,负序电流只与负序电压有关系[6]。 根据上面的分析,系统的控制结构框图如图2所示。电源电压经DQ变换后经低通滤波后得到正序电压分量与负序电压分量。电流检测经DQ变化后经100HZ带阻滤波器后得到电流正序分量与电流负序分量。这里选择带阻滤波器主要是考虑到在本系统反馈通道中采用低通滤波会因此系统振荡。
图2 系统控制结构 
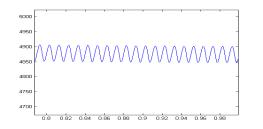
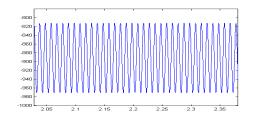
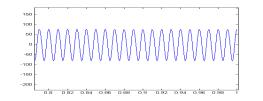
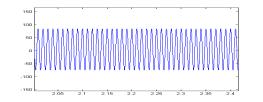
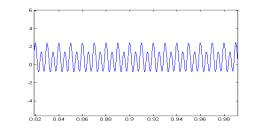
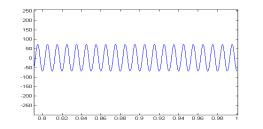
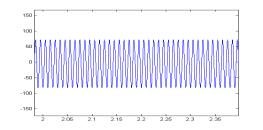
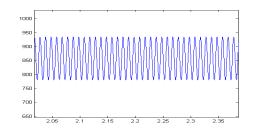
图3给出采用本方案和采用本方案和常规DQ变换控制方案时系统各功率分量的对比。常规控制时,IQ=0。图中(a-1)~(a-7)为采用本方案的功率仿真结果,(b-1)~(b-7)为采用常规DQ变换控制的功率分析结果。通过对比可以看出在常规控制时瞬时无功瞬时无功 4 结 论 本文分析了系统瞬时无功分析在三相PWM功率因数校正系统中的应用,通过对比我们可以看出,当我们对系统各无功分量的进行控制时,可以有效减少系统瞬时无功,这对消除系统瞬时无功对系统带来的消极影响是卓有成效的。 参考文献: [1] 马大铭,朱东起,高景德,三相不平衡时谐波和无功电流的准确检测,清华大学学报,1997年,No.4,p7-10 [2] 刘进军,王兆安,瞬时无功功率与传统功率的统一数学描述及物理意义,电工技术学报,1998年12月p6~13 [3] 三相电路瞬时电流功率分解与PARK空间变换,浙江大学学报,2001年,No1,14~16。 [4]P.Rioual,H.Pouliquen,and J.Louis, “Regulation of a PWM rectifier in the unlalanced network state using a generalized model”, IEEE PE vol 11 pp495~502, May 1996 [5] Hong seok Song, Kwanghee Nam, Dual Current Control Scheme for PWM Converter Under Unbalanced Input Voltage Conditions. IEEE IE vol 46 No.5,953~959,1999 [6] D.Beeman, Industrial Power System Handbook. New York:McGraw-Hill, 1955 作者简介: 孙孝峰(1970出生于黑龙江省),1999年获得燕山大学控制理论与控制工程硕士学位,目前攻读燕山大学电路与系统专业博士学位,主要研究方向为高频功率变换与太阳能逆变技术。 邬伟扬(1940出生于上海),燕山大学教授,博士生导师,电力电子学会理事,主要研究方向为高频功率变换与电力电子系统故障保护,发表文章60余篇。
|
||||||||||||||
| 作者:孙孝峰 邬… 来源:电源技术应用 点击数: |
| - | 【字体:小 大】 |


 (23)
(23)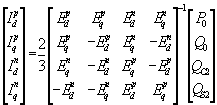 (24)
(24)  (25)
(25)