|
【字体:小 大】 |
| 多路输出正激式变换器耦合滤波电感的设计 | |
| http://www.dykf.com 2008/5/30 电源开发网 | |
|
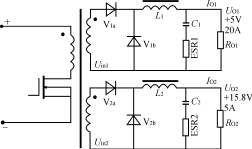
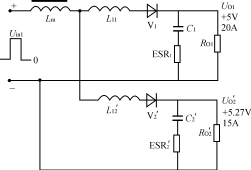
1引言 近年来高频开关电源在电子产品中得到广泛应用。正激式DC/DC变换器以其输出纹波小、对开关管的要求较低等优点而适合于低压、大电流、功率较大的场合。但正激变换器对输出电感的设计有较高要求,特别在多路输出的情况。 本文分析对比正激变换器多路输出滤波电感采用独立方式和耦合方式的不同特点,讨论了耦合电感的设计方法,给出了一个设计实例,并给出仿真及试验结果。 2正激变换器普通多路输出的分析 图1所示为180W正激变换器的变压器及输出部分。两路输出分别采用无耦合的滤波电感。其一路输出UO1为:UO1=(Uin1-UV1a)D-UV1b(1-D)=Uin1D-UV1b(1) 式(1)中,D为初级开关脉冲的占空比,UV1a、UV1b分别为整流二极管和续流二极管的压降,并假设它们相等。 该电路L的最小值一般由所需维持最小负载电流的要求决定,而电感L中的电流又分连续和不连续两种工作情况。如果负载电流IO逐步降低,L中的波动电流最小值刚好为0时,即定义为临界情况。在控制环中,连续状况的传递函数有两个极点,不连续状况只有一个极点。因而在临界点上下,传递函数是突变的。图1电路的Uin1,Uin2绕组通常都为紧耦合状态,而每一路LC滤波器的串联谐振频率不相同,这一情况将使控制环在连续状况时传递函数增加新的极点。 在多路输出时,如果辅助输出电压要保持在一定的稳定范围内,则主输出的电感必须一直超过临界值,即一直处于连续状态。从性能上讲,L过大限制了输出电流的最大变化率,而且带直流电流运行的大电感造价昂贵。 在图1所示的电路中,当UO1保持5V不变时,随着UO2负载上的突然变化,其15.8V的电压有可能突变4V~5V,且在经过数十至数百毫秒后才能恢复。
图1独立滤波电感两路输出正激变换器
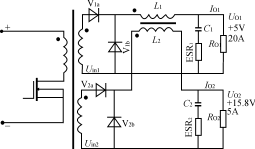
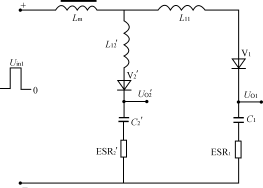
图2耦合滤波电感的两路输出正激变换器
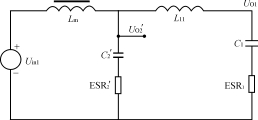
图3
图4 图3电路的归一化电路
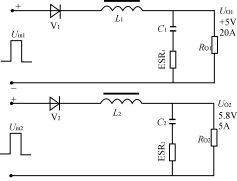
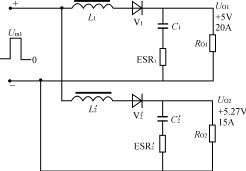
图5 图4电路的重新排列 为了简化设计,通常都使电感电流工作于连续状态。当负载电流变化较大时,甚至在出现负载电流为零的场合下为使电路仍可以正常工作,则可在每路输出接入一固定负载。 3多路输出正激变换器耦合滤波电感的分析 对照图1和图2电路,图2电路的L1、L2为绕在同一磁芯上的电感,且匝数比与Uin1、Uin2的匝数比相同,同名端如图所示。 设:UV1a=UV1b=UV1=0.6V UV2a=UV2b=UV2=1.0V D=0.4UO1=5Vn=N2/N1=3:1 则有:Uin1=(UO1+UV1)/D=5.6V/0.4 =14Vpp(2) Uin2=Uin1·n=14×3=42Vpp(3) UO2=Uin2·D-UV2=42×0.4-1.0=15.8V 在初级开关管导通时 UL1=Uin1-UV1-UO1=14-0.6-5=8.4V(4) UL2=Uin2-UV2-UO2=42-1.0-15.8=25.2V(5) 在初级开关管截止时 UL1=-UD1-UV1=-0.6-5=-5.6V(6) UL2=-UD2-UV2=-1.0-15.8=-16.8V(7) 注意:不论初级开关管导通还是截止,应保证UL2/UL1总是为3∶1。如果耦合电感L2、L1的匝数比不能保证为3∶1,则在UO1和UO2之间存在附加的电流流动,从而在其输出产生很大的输出纹波。〔3〕 为了便于分析,将图2中主变压器的两个输出绕组用两个脉冲电压源所取代,则可简化如图3所示。再将图3电路归一化,如图4所示。 图4电路中,N2′=N2/n=N1 Uin2′=Uin2/n=Uin1 UV2′=UV2/n=1/3=0.33V UO2′=UO2/n=15.8/3=5.27V IO2′=IO2·n=5×3=15A L2′=L2/n2 C2′=C2·n2 ERS2′=ERS2/n2 图2至图5的归一化简化分析适用于独立电感和耦合电感的情况。对于耦合电感电路,图5中的L1和L2′在同一个磁芯上有相同的归一化匝数,因此它有相同的归一化互感值及相同的感应电压/匝数比。因此L1和L2′可合成一个互感Lm,如图6所示。
图6电路的互感、漏感等效电路
图7 纹波电流进入U02‘的情况
图8 图7电路的归一化小信号模型
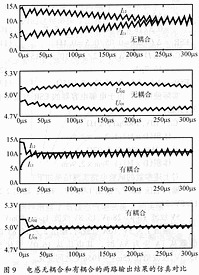
图9电感无耦合和有耦合的两路输出结果的仿真对比 由于电感的耦合不是百分之百,总存在漏感及外部电路的引线电感。这种影响可用L11和L12′表示。实际上Lm比L11或L12′大得多。即使在开关频率上,Lm的阻抗值比输出电容(包括ESR)的阻抗值也大得多。所以,归一化纹波电流总的大小由Lm决定。而进入各路输出的纹波电流则由L11和L12′决定。换言之,归一化纹波电流可以不同的比例分别流入不同的输出,甚至可以一路的归一化纹波电流为0,这完全取决于图6电路中L11和L12′的值。 如果希望纹波电流大部分流入高压输出UO2′这一路,则要求L12′比L11小得多。归一化电路如图7所示。对耦合电感进行特殊的工艺设计,就可以达到以上的目的。为了使低压输出UO1的漏感较大,可使UO1的滤波绕组位于电感的内层,而UO2的绕组位于外层,就可达到以上的目的。对于EE型铁氧体磁芯,漏感量通常小于互感量的10%,如果两个绕组双线并绕,该值约为2%。 图8为图7电路的归一化小信号模型。由于L12′较L11小得多,为简化分析,可忽略L12′,并假设UV1、UV2为0。在图8中,互感Lm和C2′组成主LC滤波器,而由L11和C1组成附加的LC滤波器。而如果附加的L11、C1滤波器的Q值大于1,控制环可能产生不稳定。特别是如果选定15V输出(UO2)作反馈环,虽然15V输出控制稳定,5V输出(UO1)有可能在L11-C1的谐振频率上产生自激。所以应使L11、C1滤波器Q值小于1。如果选定5V(UO1)作反馈环,则电路为两级LC电路控制,有可能产生180°的相移。由于Lm较大,采用电流控制方式时,将使第一节LC电路远离90°的相移,对系统的稳定性十分有利。 4仿真结果 对无耦合和有耦合电感的两路输出正激变换器的仿真电路分别按图1、图2进行。 为便于观察,设UO1为5V、10A,UO2也为5V、10A,主控网络为UO1,开关频率f=100kHz,L1=L2=10mH,有耦时,耦合系数为0.95,电感量L11=0.5μH,且位于UO1输出,C1=C2=3000μF,ESR1=ESR2=0.1Ω 仿真结果如图9所示。 5设计实例 图2电路中,输出1:5V,20A100W 输出2:15.8V,5A80W 归一化输出2:5.27V,15A80W 首先决定主变压器输出绕组和耦合电感的匝数比。 N2∶N1=(15.8+1)∶(5+0.6)=16.8∶5.6=3∶1(8) 初级MOS管截止时计算电感量,占空比最小(D=0.25)时,对100kHz开关频率,最大截止时间Δt=7.5μs,最大纹波电流ΔIm=6A(满载电流的17%),则有: Lm=E·Δt/ΔIm=5.6×7.5/6=7μH(9) 设5V输出端的漏感为700nH(7μH的10%),附加100nH的引线电感,则L12′为11nH(=100nH/n2),则IL的分配为: 输出1:6A·11/(800+11)=0.08App 归一化输出2:6A·800/(800+11)=5.9App 输出2:5.9A/3=2App 设最小负载电流(ΔI), 输出1:0.5A 输出2:2A 最大输出纹波(ΔU)要求 输出1:0.05V(输出的1%) 输出2:0.15V(输出的1%) 则 C1=(ΔI)/(8fΔU) =0.5/(8×105×0.05)=12.5μF(10) ESR1=ΔU/ΔI=0.05/0.5=0.1Ω(11) C2=(ΔI)/(8fΔU)=2/(8×105×0.15) =16.7μF(12) ESR2=ΔU/ΔI=0.15/2=0.075Ω(13) 实际使用中,由于电解电容器的ESR与直径有关,实选: C1:10V,1000μF,0.1Ω 体积(D×H):1.3cm×2.9cm C2:25V,470μF,0.07Ω 体积(D×H):1.7cm×2.9cm 对上述参数的试验电路实测结果如下: 输入电压220V,输出1为5V、10A;输出2为15.8V、3A。 5V纹波Vpp=28mV,15.8V纹波Vpp=80mV。 当输出1为5V、10A负载时,输出2为15.8V的负载从1A变为5A时,其电压从16.0V变化至15.5V,纹波则在75mV~105mV之间变化。 6几点说明 (1)由于绕制工艺的不同,漏感将在很大范围内变化,为控制2%~10%的漏感范围,最好采用罐形或环形磁芯,双线并绕,低压绕组在里层,或“三明治”绕法,将低压输出滤波绕组夹在高压输出滤波绕组之间,低压输出的纹波将大大减小。 (2)在前述的分析中,整流、续流对管不可能完全对称,而两路输出的对管的正向压降也会不同。这种不同只会影响输出电压的大小,而对纹波电流的影响,则可通过前述的“漏感”方法予以消除。 (3)上述“漏感”方法有时不易控制,可以用耦合电感匝数的小量变化获得同样的效果。对于纹波要求较小的那一路输出的绕组匝数,可乘以110或105的系数。 如果另外加一个独立的小电感,也可以获得同样的效果。 (4)上述的分析是以两路输出同为正电压进行的。如果一组输出为负,则耦合电感的同名端应予变化。对于双线并绕的情况,只要将一组绕组的出端与入端对调即可。只是这种对调使两个绕组中的电流方向相反,因而会产生附加的纹波电流。所以实际的绕制工艺,应一组采用顺时针方向绕制,另一组采用反时针方向绕组,这样可获得最佳效果。 (5)上述两路输出的分析也适用于三路或更多路输出的情况。但首先要满足电感的匝数比等于主变压器的输出绕组的匝数比,再考虑漏感对纹波的影响。 (6)本文分析的耦合滤波电感的原理也适用于BUCK型的半桥及全桥拓朴。但对于辅助输出再接另一级PWM稳压器或磁饱和稳压器的拓朴形式,则特性及纹波的改善并不明显。 您打印的此文来自: |
|
| 作者:余大武 石… 来源:《电源技术应用》-2003年6卷3期 点击数: |
| - | 【字体:小 大】 |