0 引言
近年来,非线性负荷的广泛应用对供电质量造成了严重污染,电力系统中的谐波日益严重,同时,保证电网安全、稳定运行,为用户提供高质量的电能的要求也越来越高。有源电力滤波器作为抑制谐波的有效手段,得到了广泛的重视并取得了很大的发展。有源电力滤波器的实质就是一个任意波形发生器[1],通过一定的算法检测到负荷侧所需要的谐波电流,就发出相应的谐波电流,从而达到补偿的目的。经补偿后系统电流将接近理想的正弦波。为了实现这一目标,需要采用适当的控制策略来控制逆变器开关。目前常用PWM和滞环控制产生开关决策以控制逆变器,对要求的电网电流都是开环的。这就意味着即使补偿电流的检测和计算非常准确,也很难保证对电源电流的精确跟踪,达到良好的调节补偿效果。因此,以并联有源电力滤波器为控制对象,在建立其数学模型的基础上,结合变结构控制和滑模控制的优点,提出了一种综合控制方法。通过使用滑模变结构控制对开关器件进行“开”或“关”状态调节。
1 并联型有源电力滤波器(SAPF)数学模型
SAPF的原理在大量文献中已有详尽说明[2][3],这里只作简单介绍。图1所示为并联型有源电力滤波器原理图。图1中交流侧的电感用于滤去载波分量;同时又作为惯性环节。直流侧的电容主要起能量缓冲的作用。由前面的分析可知,当ic和负载电流iL合成产生一个与电源相电压几乎同相位的正弦波电流时,电网的功率因数便接近于1。假设主电路三相电源对称且稳定,开关器件IGBT为理想开关,其控制用开关函数描述,开关函数可定义为
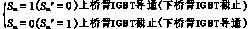 (m=a,b,c)(1)
(m=a,b,c)(1)
图1 并联型有源电力滤波器(SAPF)原理图
其状态方程为
Z =AX+BE(2)
=AX+BE(2)
式中:X=[ica icb icc Uo];
E=[ua ub uc 0];
Z=diag[L L L C];
B=diag[1 1 1 1/R];
A= ;
;
La=Lb=Lc=L为SAPF侧滤波电感;
R为SAPF侧电容等效电阻。
根据图1的电路结构图可得到式(3)微分方程。
L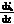 =us-SmUo+L
=us-SmUo+L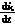 (3)
(3)
L=[La,Lb,Lc],us=[ua,ub,uc],iL=[iLa,iLb,iLc]
式中:L为SAPF的电感;
us为电源电压。
由于SAPF的作用是通过逆变器输出把电源电流is调解成与电源电压us同相位的正弦波作为控制系统的设计目标。假设电源电压为正弦波,设定电源电流的给定值is*为
is*=kus(4)
式中:k为一标量,其大小决定于负载有功功率和SAPF所消耗的有功功率,这将由逆变器直流侧电容电压的闭环控制来调整。
于是采用SAPF进行电网补偿的问题,转化为如何使电源电流is很好地跟踪参考给定电流is*。采用变结构控制时可定义状态变量为
Δis=is*-is=kus-is(5)
整理式(3)、式(5),可得状态方程
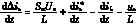 (6)
(6)
定义
e=-L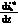 +L
+L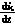 +us(7)
+us(7)
则状态方程(6)可以写为
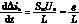 (8)
(8)
式(8)可以详细写为

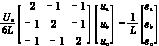 =(9)
=(9)
2 滑模变结构控制器设计
2.1 可达性条件
根据滑模变结构理论[4],定义滑模切换线为
s=is*-is=kus-is=Δis(10)
根据变结构可达性条件,必须满足s <0
<0
即 Δis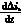 <0(11)
<0(11)
也就是
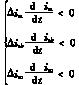
SAPF的变结构控制率为
um=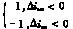 (m=a,b, c)(12)
(m=a,b, c)(12)
2.2 等效连续控制
当系统进入滑动模态时满足条件[5][6]
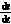 =0(13)
=0(13)
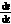
 =(14)
=(14)
由图1可知
us=L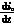 +UoSm(15)
+UoSm(15)
由式(13)、(14)、(15)可以求得等效控制
veqk=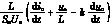 (16)
(16)
由于-1(<=)veqk(<=)1,如果系统在满足式(16)和开关频率无限高的情况下,控制逆变器开关,可以使系统工作在切换线上,这样is将紧紧跟踪is*。虽然实际系统不可能工作在无限高的切换频率下,按-1(<=)veqk(<=)1进行控制的系统不可能始终工作在滑模切换线上,但总能保持趋向于切换线而不受外部扰动的影响。
2.3 稳定性分析
当系统状态点未到达滑模切换线时,定义李雅普诺夫函数为
V(x)=s′s=x′x(17)
分析可知上式是正定的。则
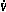 (x)=
(x)= =2x′
=2x′ =2
=2 =2
=2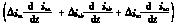 (18)
(18)
根据式(11)可知
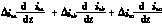 <0,所以
<0,所以
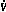 (x)<0(19)
(x)<0(19)
当系统状态点到达滑模切换线时,
 (20)
(20)
由此,可以看出滑模变结构控制策略在SAPF中的应用有它的理论依据。
3 SAPF的控制系统
系统的控制框图如图2所示,直接将电源侧的输入电流is作为控制对象,使其为正弦波,且与电源电压同相,达到功率因数为1的目的。系统采用双闭环控制,外环为电压环,一方面控制直流侧的电压使其稳定在给定值附近,另一方面,根据有功功率的流动并利用功率平衡获取参考输入电流的幅值k,与同步信号相乘后作为电流参考信号is*。内环是电流环,检测实际输入电流is与参考电流is*的误差,其误差经SMC控制电路产生相应的PWM波控制电路中各个开关管的导通和截止,从而达到实时跟踪控制电源实际电流的目的。控制中,外环电压环采用PI控制。另外,为了避免同一桥臂上两个功率器件在换流时出现的瞬间短路,电路设计上还设置了死区延时,以保证同一桥臂上器件顺序通断。

图2 SAPF的变结构控制原理图
4 仿真与实验验证
4.1 仿真验证
为了验证本文中所论述的控制策略的正确性,先将本文所提出的方法用Matlab中的SIMULNK进行了仿真验证。仿真条件为:电网电压150V,工频50Hz;三相有源滤波器的电容C=3300μF,电感La=Lb=Lc=5mH,非线性负载为三相全桥整流电路,直流侧LL=100mH,RL=17.8Ω。为说明SMC控制策略的优越性,除了对SMC仿真外,在相同条件下还用电流滞环比较法进行了仿真。负载电流波形如图3所示,电流滞环控制策略波形如图4所示,SMC控制策略所得波形如图5所示。从图中可以看出,使用SMC控制方法时,不仅直流侧电容电压稳定快,而且并联型有源滤波器也取得了良好的补偿性能,交流侧电流已比较接近理想正弦波形了。
(a) 负载电流波形
(b) 补偿电流波形
图3 SAPF负载侧电流波形

(a) 直流侧电容电压波形

(b) 补偿后网侧电压电流波形(幅值大的为电压,小的为电流)
图4 常规控制策略所得波形
(a) 直流侧电容电压波形
(b) 补偿后网侧电压电流波形(A相,幅值大的为电压,小的为电流)
图5 SMC控制策略所得波形
4.2 实验验证
当有源电力滤波器补偿不同大小的三相不控整流负载的谐波与无功电流时,补偿电流与?偿后网侧电流波形如图6所示。
(a) 负载电流波形
(b) 补偿后网侧电流波形
(c) APF所发出的电流波形
(d) (a)、(b)、(c)三者电流波形汇总
图6 实验波形汇总〔横坐标5ms/div,纵坐标10A/div〕
5 结语
采用滑模变结构控制可以避免补偿电流给定值is*的复杂计算,使控制变得简单且易于实现。由于实现了对is*跟踪的闭环控制,故可获得良好的调节性能。仿真和实验结果表明,此方法不仅加快了系统的响应速度,而且实现简单明了,能有效地增强控制系统的稳定性,改善系统的动、静态性能。提出的基于滑模变结构控制的并联型有源电力滤波器在不增加硬件成本的条件下取得了较常规方法更优良的补偿性能,有一定的应用前景。
