反激式电流谐振型功率因数校正电路的研究

赵志伟   南京气象学院 电子物理系(南京 210044)

摘要：提出了一种具有零电流关断（ZCS）的反激式单级功率因数校正（PFC）变换器。 这种变换器工作在完全能量转换方式(DCM)，综合了电流谐振技术与PFC技术。分析了这种变换器的工作原理，并在输出30W条件下进行了实验验证。

关键词：反激式变换器  功率因数校正  电流谐振

Research on a Flyback Converter With ZCS Resonant and PFC

Abstract: A flyback converter with zero current switching (ZCS) resonant and power factor correct （PFC）is proposed. It is a single-stage converter operated at discontinuous conduction mode(DCM). It combines the technique of current resonant and PFC. The working principle has been analyzed. Experimental verified results are present under output power 30W.

Keywords： Flyback converter， Power factor correct， Current resonant

1  引  言

传统的交-直流（AC-DC）变换是在输入端使用二极管和电容进行整流滤波，这样会产生大量的电流谐波，功率因数也较低。因此，需要加上功率因数调节电路。目前，有两级功率因数调节和单级调节两类电路。单级功率因数调节使PFC和DC/DC共用一个开关管，仅用一套控制电路，同时进行输入电流的整形和输出电压的调节。由于采用脉宽调制（PWM）的电压控制方式，当开关器件的工作频率大于100KHz时，会产生较大的开关损耗[1]，降低了单级功率因数电路的效率。因此，针对上述情况，本文研究了工作在35KHz的反激式电流谐振型PFC变换器，并给出了实验结果。

2  变换器稳态工作分析

图1是反激式零电流关断（ZCS）准谐振变换器的原理图，其电路的工作波形示于图2，每个开关周期被分成六个工作模式，对应这六个工作模式的电路状态图示于图3。

设电路已处在稳态，并有：

1)     关管Q是理想器件；

2)     耦合电容上的电压是恒定的直流电压VC；

3)     输出电压是恒定的直流电压VO；

4)     变压器的电感量非常大，可视为一个恒流源。

    模式1： （t0<t£t1，图3(a)） 开关管Q在t=t０时导通，由于谐振电感电流iLr(t)是小于反馈回变压器原边的磁化电流I2/n，整流二极管D3处于导通状态，谐振电容Cr上的电压VCr(t)被输出电压Vo箝位，iLr(t)线性增加，可用下式表达：

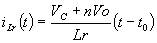       (1)

电感L1电流也随着 线性增加，有下式：

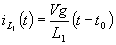                                 (2)

当ILr(t) 达到 时，第一阶段结束。这段时间可表达为：

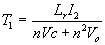                                   (3)

    模式2：(t1<t£t2，图3(b)) 随着谐振电容Cr释放能量给谐振电感Lr， 整流二极管D3反偏截止，谐振电容Cr上的电压Vcr(t)以正弦方式减少，因为有下式：

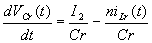      (4)

谐振电流增加的速率为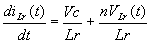：      (5)

初始条件是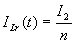： ，所以有

    (6)

上式中 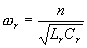， ，这一阶段的电感电流iL1呈线性上升，可表为：

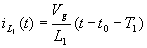        (7)

开关电流iQ将继续按正弦规律变化，并反馈能量给耦合电容。当iQ =iL1(t)+ iLr(t)=0时第二阶段结束。这段时间用T2表示。 

模式3：(t2<t£t3，图3(c)) 在t=t2时开关管关断，因谐振电感Lr中的电流不能突变，二极管D2仍处于导通状态，为iLr 提供通道，同时，D1也开始导通，将L1上的能量传递给耦合电容C。这样，由iLr(t)和I2/n通过D1和D2给谐振电容Cr充电， 谐振电感Lr上的电流和谐振电容Cr的电压继续按正弦规律变化。又因为开关管已关断， 开关管漏源间的电压等于耦合电容上的电压。在这一阶段的时间里，电感L1上的电流iL1(t)开始线性下降，有下式：

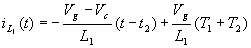         (8)

当VCr(t)=Vo时，这一阶段 (称为T3)结束。

模式4：(t3<t£t4，图3(d)) 这一阶段中，二极管D1和D2保持导通，开关管漏源间的电压仍等于耦合电容上的电压。 电感L1上的电流IL1(t)继续线性下降。输出滤波电容Co与谐振电容Cr并联。VCr(t)被VO箝位，谐振电感的电流iLr在这一阶段线性增加，并经过变压器提供给负载，当iLr到达零点时，模式4 (称为T4)结束。

    模式5：(t4<t£t5，图3(e)) 这一阶段电路的工作方式与传统的反激式变换器工作原理相同。当输入的电感电流iL1(t)减少到零时。这一阶段(称为T5)结束。

输入电感电流iL1(t)由零到下一开关周期TS的开始，称为模式6：(t5<t£t6)，见图3(f) 。

由以上的分析，可以得到下面的结论：

输入（电感）电流iL1(t) 的线性上升和下降仅由输入端的电压Vg和耦合电容电压VC决定，不受开关管的ZCS影响， 输入平均电流为[1][2]：

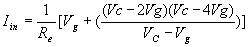       (9)

式中等效输入阻抗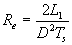：  ，呈现阻性。

占空比： ，TS是开关器件的工作周期。这说明了：

1)输入平均电流与入端电压之间满足欧姆定律；

2)在ZCS且输入电流为DCM模式下工作时， DC-DC反激变换器的输入阻抗是由开关频率占空比D控制的电阻Re。

3)输入端的电压正弦变化时，输入电流也按正弦变化，功率因数接近于1。

3  参数设计和器件选择

为保证在每个开关周期的开关导通期间产生满足DCM条件下的电流谐振ZCS，必须合理选择产生谐振的元件Lr 、Cr以及输入电感L1。

1）由上面的理论分析知：在模式2时流过开关管的电流是谐振电流ILr与经过D2的输入电流IL1之和。在t2时应降到零，也即式（6）、（7）之和为零：

    (10)

上式中的正弦函数若为负值（比如：-1），或者第二项中的特征阻抗Zr较大，对开关器件的电流冲击就会较小。

考虑到变换器的效率η，根据文献[1]，有下式：

        （11）

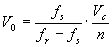                 （12）

由式（3）、（10）、（11），选择谐振元件Lr 、Cr ，由式（11）、（12）选择变压器的匝比n。

2）为保证输入电流工作在DCM状态， 电感L1不能选的太大，应满足在一个开关周期里的T1+T2≤Tr ，同时满足下式[1]：

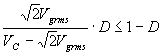             （13）

因此，由式（11）、（12）、（13）可确定输入电感L1。

3）开关管上承受的电压是：Vds=Vc+nVo, 由式（11）、（12）知负载较轻（R比较大）、开关频率较高时，开关管的电压应力较大。而负载满载且输入为峰值电压时，开关管的电流应力较大。由理论分析知：电流达到正的最大值是发生在模式2（T2阶段）谐振周期的1/4处。有下式：

        （14）

根据式（11）~（14），综合考虑开关管的电压和电流应力问题，合理选择开关器件。

4  实验结果

在输入电压Vg rms =56V，输出电压Vo =18V，输出功率Po=30W条件下进行了实验。

电路参数：考虑到变压器的漏感和开关器件的寄生电容，选择工作在电流不连续（DCM）状态下的电感L1≈156uH，谐振电容Cr≈0.047uF，谐振电感Lr ≈120uH，变压器的匝比n=N1/N2≈3，开关管选用IRFP460，由SG3525组成PWM控制电路，开关管的工作频率为35 KHz。取样电压来自负载的取样电阻R2。

使用型号为POS9020示波器测得的有关波形见图4、5和6。图4是电路中开关管的漏源电流iQ和漏源间电压Vds波形，图5是谐振电容上的电压VCr波形，与理论分析基本一致。图6是在输入端采样到的电压、电流波形，从图中可以看到电压与电流基本上同相，实测的功率因数≈0.94，效率为89%。谐振频率fr=80KHz。

5  结  论

（1）工作于DCM模式下的反激式电流谐振型DC-DC变换器，具有绝缘隔离、电路简单、成本低的特点。将电流谐振技术与PFC技术结合，开关管导通和关断时的功耗都较低，提高了DC-DC变换器的效率。

（2）因采用了PWM集成电压型控制电路，稳态时占空比恒定，输入电流能自动跟随输入电压变化，这又提高了电路的功率因数。由于反激式PFC变换器电路的特点[2]，这种电路仅适合于小功率且负载变化较小的应用场合。

（3）存在问题：由于输入电流的DCM状态，电路的电磁干扰（Electromagnetic Interference 简称EMI）比较高，在设计中必须要加以考虑；另外，开关管的电压应力相对较高，这也是需要解决的问题。

参考文献：

[1] Jun-Young Lee，Integrated ZCS Quasi-Resonant Power Factor Correction Converter Based on Flyback Topology，IEEE TRANSACTIONS ON POWER ELECTRONICS.VOL.15, NO.4， JULY 2000:634~643。

[2] 张占松, 蔡宣三。开关电源的原理与设计。北京:电子工业出版社，1998。

[3] 许化民，阮新波，严仰光。单级功率因数校正AC/DC变换器的综述。电力电子技术， 2001(1): 56~60。

[4] 叶治政，叶靖国。开关稳压电源。高等教育出版社，1989。

作者简介：

图4  开关管电流iQ(上)与漏源电压Vds波形

(iQ:0.8A/div,Vds:50v/div,10uS/div)

Fig. 4 Experimental waveforms of iQ and Vds

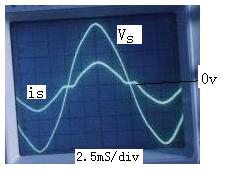
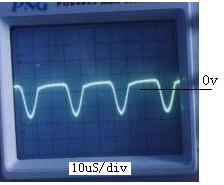
图5谐振电容电压Vcr的波形(20V/div)        图6 输入端电压Vs(20v/div),电流is(0.2A/div)波形

Fig. 5 Experimental waveform of Vcr        Fig. 6 Experimental waveforms of Vs and is