开关电容DC/DC变换器的理论研究
刘术平,梁冠安,彭军
(华南理工大学电力学院雅达电源实验室,广东 广州 510640)
Abstract:The switched-capacitor DC/DC converters contain no magnetic components, so they can be miniaturized and suitable to be manufactured as IC systems, offering a good approach for low power supply.The principle and standard model of the switched-capacitor DC/DC converters,as well as the control methods are described,The efficiency of the converters is discussed. The prospect of the converters is looked ahead.
Keywords:Switched-capacitor; DC/DC converter; Equivalent electric-quantity relation method (EEQR)
1 引言
上世纪70年代后期以来,随着集成电路设计与制造技术的进步,各种用电设备逐渐向小型化方向发展,相应地,研究与之配套的体积小,重量轻,效率高的电源已成为人们感兴趣的重要课题。传统的开关电源采用软开关技术,通过提高开关频率可以缩小电源的体积,但是由于结构中含有电感和变压器,因而限制了电源体积的进一步缩小。如今虽然已有片状电感问世,但仍然不能令人满意。近年来,人们提出了一种新型的开关电容变换器,这种变换器结构中不含电感和变压器,仅由电容网络和开关管构成,因此可望进一步缩小电源的体积,甚至在芯片中实现集成,基于这些显著的优点,这种变换器愈来愈引起人们的广泛兴趣。
2 开关电容DC/DC变换器的统一模型及工作原理
开关电容DC/DC变换器的统一模型如图1所示,图中S代表功率开关,Ci代表ni阶的串并电容组合结构,阶数ni为其中的电容个数,下标i代表第i级串并电容组合结构。串并电容组合结构是由电容(通常取值相同)和二极管构成的,其中的电容具有串联充电,并联放电的特性,如图2虚线框中为二阶串并电容组合结构,图3为基本的开关电容DC/DC变换器。
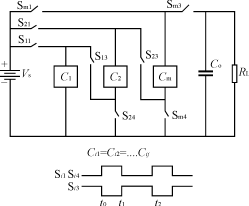
图1 开关电容DC/DC变换器的统一模型
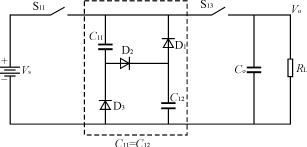
图2 二阶串并电容组合开关电容DC/DC变换器 (SP-SC)

图3 基本开关电容(BSC)DC/DC变换器
在状态I,Si1和Si4导通,Si3截止,C1....Cm并联充电,而根据串并电容组合结构的特点,构成Ci的ni个电容Cij却呈串联状态;同样地,在状态II,Si1和Si4截止,Si3导通,C1....Cm串联放电,而构成Ci的ni个电容Cij却呈并联状态。在状态I,Co放电提供负载电流,在状态II,C1....Cm向Co补充电量。同时Co起到输出滤波的作用,这样便能得到一个平滑的输出电压。
3 开关电容DC/DC变换器的分析方法
3.1 状态空间平均法
状态空间平均法的基本思想就是先确定几个状态变量(一般为电容电压或者电感电流),将电路在一个工作周期之内分成几个不同的工作状态,分别列写在每一状态下电路的状态方程,再综合考虑各个状态下的状态方程,求出一个平均状态方程,求解这个平均状态方程即可解出各个状态变量对时间t的关系函数,于是电路中的各个变量(节点电压或支路电流)即可求出。
状态方程的一般矩阵形式为
 =AjX+Bje j=1,2,3…
=AjX+Bje j=1,2,3…
Y=CiX
式中:X=[X1X2 Λ Xm]T,e=[Vs1Vs2 Λ Is1Is2 Λ Isk]T
现以图2的二阶开关电容DC/DC变换器为例,说明利用状态空间平均法分析开关电容变换器的具体过程。
设C11=C12=C,输出滤波电容Co,电容C11和C12的串联寄生电阻为r,开关管的通态电阻为r′,二极管的正向压降为Vd,电源内阻及输出电容的寄生电阻忽略不计,状态变量x1,x2,x3分别为Vc1,Vc2,Vco;e=[VsVd]。
则状态I时
A1=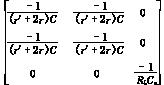 ;
;
B1=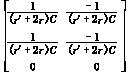
状态II时
A2=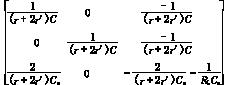 ;
;
B2=
平均状态方程的系数矩阵为
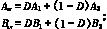 D=
D=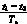 为开关S11的占空比;Ts为工作周期;求解该状态方程即可得出各个状态变量的解,即Vc1=f1(t),Vc2=f2(t),Vco=f3(t),输出电压Vo=Vco=f3(t)。
为开关S11的占空比;Ts为工作周期;求解该状态方程即可得出各个状态变量的解,即Vc1=f1(t),Vc2=f2(t),Vco=f3(t),输出电压Vo=Vco=f3(t)。
3.2 等效电量关系法
利用状态空间平均法虽然可以较为精确地分析开关电容DC/DC变换器,但是当电路较为复杂时,如其中含有较多的电容元件或者工作状态较多时,建立以及求解平均状态方程将是一件极为繁琐的工作。利用开关电容DC/DC变换器结构上的特点,可以得到更简化的分析方法,我们称之为“等效电量关系法(EEQR)”。
现以图1的统一模型为例,介绍这种分析方法。
设Ri为在状态I期间Vs对Ci充电的等效阻抗,r是电容器的等效串联阻抗(ESR),r′为开关管的导通电阻,则有
Ri=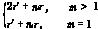 (1)
(1)
设Qi′和Qij′分别为Ci和Cij在状态II放掉的电量,也即负载在一个周期内通过的电量;设Qi和Qij分别为Ci和Cij在状态I的充电电量,由于构成Ci的各个电容Cij串联充电,并联放电,所以有
Qi=Qij
Qi′=niQij (2)
Cij在状态II失去的电量,应在状态I得到充分地补充,于是
Qij=Qij′
Qi′=niQi (3)
根据电容,电量和电压的关系(Q=CU),有
Vci(t1)-Vci(t0)= (4)
(4)
而
Qi′=ILTs= (5)
(5)
根据在状态I期间,电容电压按指数规律上升的原则,有
Vci(t1)-Vci(t0)=[Vs-(ni-1)Vd-Vci(t0)][1-exp(-DTni/RiCij)](6)
由以上各式可以推出
Vci(t1)=Vs-(ni-1)Vd- (7)
(7)
假设Co很大,即Vo的纹波很小,在状态II结束时,则有
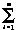 Vci(t0)/ni-
Vci(t0)/ni-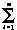 (ni-1)Vd=Vo(8)
(ni-1)Vd=Vo(8)
从而可以得到:
Vo= (9)
(9)
将式(9)的指数项展开成幂级数,并忽略二次以上各项,则有
Vo= (10)
(10)
式(10)即为脉宽调制(PWM)下,典型开关电容DC/DC变换器的稳态电压的通用表达式。
4 开关电容DC/DC变换器的控制方法
式(9)中,我们称DTsni/RiCij为该串并电容组合结构的特征系数,用Ki表示,根据Ki的取值,一般可以分为以下三种工作情况。
1)脉宽调制模式(PWM)
当各个串并电容组合结构的特征系数Ki均较小时,式(9)中的指数函数的幂级数展开式的二次以上各项可以忽略不计,从而式(9)可简化为式(10),式(10)表明采用PWM方式,可以获取调制效果,改变工作频率对于变换器的输出电压没有明显影响,我们称之为脉冲宽度调制模式。
2)频率调制模式(FM)
当各个串并电容组合结构的特征系数Ki均较大时,式(9)可简化为
Vo=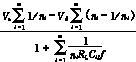 (11)
(11)
式(11)表明,采用PWM方式,已经无法获得明显的调制效果,而采用FM方式,可以起到调制输出电压的作用,我们称之为频率调制模式。
3)过渡模式(混合调制模式)
当存在至少一个串并电容组合结构的特征系数Ki不很大,也不很小时,式(9)中的指数项不能线性化,开关电容DC/DC变换器的输出电压受到工作频率和占空比的双重影响,称之为过渡模式。
一般情况下,三种工作模式的分界线可确定如下[2]:
Ki>3时,开关电容DC/DC变换器工作在FM模式;
0.2<Ki<3时,开关电容DC/DC变换器工作在过渡模式;
Ki<0.2时,开关电容DC/DC变换器工作在PWM模式。
4)逐压控制模式
PWM动态响应速度较慢,只适用于DC/DC变换器,而逐压控制方法具有较好的动态响应,采用同样结构的开关电容变换器,可实现DC/AC变换和构成失真小的DC/AC变换器。
现以图3的基本开关电容DC/DC变换器为例阐述其工作原理,控制电路原理图如图4所示。
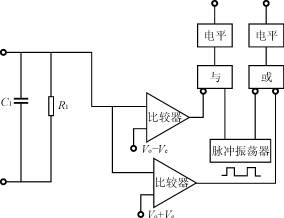
图4 基本开关电容DC/DC变换器逐压控制电路原理图
变换器启动后,当输出超过Vo+Ve或振荡脉冲为负时,S12关断,S11导通;当输出低于Vo-Ve且振荡脉冲为正时,S12导通,S11关断。Vo是输出电压设计值,2Ve为允许纹波电压峰-峰值。通过振荡器提供的脉冲信号,可以保证在变换器启动初始即使Vo很低(或为零)C1也有被充电的机会,而当Vo建立起足够的电压后,通过逻辑电路封锁振荡器脉冲。这样,在启动初期,S11,S12受振荡器强制控制,以确保启动成功,稳定后振荡器不起作用,开关管完全由输出电压反馈控制。这就是逐压反馈控制的基本原理,通过这种控制方法可以使输出电压限制在所设计的动态范围之内。
5 开关电容DC/DC变换器的效率分析
5.1 基本效率分析
从能量的角度,效率η可以定义如下:
η=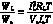 (12)
(12)
式中:WL和Ws分别是负载消耗和电源供给的能量;
IL和Is分别是负载电流和电源电流的平均值;
T为工作周期。
WL和Ws也可写作
WL=QLVL,Ws=QsVs
式中:QL和Qs分别是流过负载及电源流出的电量;
VL为负载电压。
于是,效率为
η= (13)
(13)
式中:M称为变换器的电压变比,M=VL/Vs;
K称为变换器的本征电压变比,K=Qs/QL。
在理想条件下,效率η可以为1,即M=K,但通常η<1,即M对于图1的基本开关电容变换器,则有
QL=Qs,η=M,K=1
上式表明,无论采取什么调制方式,基本开关电容变换器的效率是其电压变比,当变比很小时,变换器的效率就很低。这并不比线性变换器好多少,但是电路却复杂得多,因而没有多大实际意义。
5.2 改善效率的方法
采用串并电容组合结构可以提高开关电容DC/DC变换器的效率。以图2的二阶串并电容组合DC/DC变换器为例进行分析。
设状态I时的充电电量为Q,状态II时的放电电量为Q′,则利用等效电量关系法可得
Qs=Q=Q11=Q12
QL=Q′=2Q11′=2Q12′
K=0.5
η=M/K=2VL/Vs(14)
式(14)表明,二阶串并电容组合开关电容变换器效率在电压变比相同的情况下,比基本开关电容变换器的效率提高了一倍。同理可以推导出n阶串并电容组合开关电容DC/DC变换器的效率为η=M/K=nVL/Vs,在电压变比相同的条件下比基本开关电容变换器的效率提高n倍,且当电压变比在本征电压变比(仅由电路结构确定)附近时可以得到较高的效率,而在其它电压变比的情况下效率仍然不高,尤其在0.5<M<1的范围内,由于有M<K的限制,不能采用串并电容组合结构,因而采用单级的电容结构无法提高变换器的效率,而且由于二极管正向压降的影响,还会使效率更低。采用多级的串并电容组合结构可以进一步改善开关电容DC/DC变换器的效率,以图1的统一模型为例,可以推导出效率的公式为
η=M/K=M/ (15)
(15)
由式(15)可知,对于各种电压变比的电压变换,只要选取适当的多级串并电容组合结构,均可获得较高的效率。例如,对于+5V/+12V的升压变换,当n1=1,n2=1,n3=2时即可获得接近90%的效率。
6 结语
近年来,开关电容DC/DC变换器获得了较大的发展,各种新型拓扑和控制方法层出不穷,开关电容DC/DC变换技术也逐渐走向成熟,由于受到电容器制造技术的限制,这种变换器只适合于小功率的电压变换。随着科学技术的不断进步,在不久的将来,开关电容DC/DC变换器必将在诸如航空航天电器、医疗仪器、机器人、通信设备、便携式电脑等领域获得广泛的应用。
参考文献
[1] On-Cheong Mak, Yue-Chung Wong and Adrian Ioinovici.Step-up DC Power Supply Based On a Switched-Capacitor Circuit[J].IEEE Trans.Ind.Electronics,1995,42(1):90- 97.
[2] T. Umerno, K. Takahashi,F. Ueno, T. Inoue, and I.Oota. A New Approach to Low Ripple noise Switching Converters on the Basis of Switched-capacitor Converters[C].in Proc.IEEE Int.Symp. on Circuit and Syst,Singapore,June 1991:1077- 1080.
[3] 刘健,陈治明,钟彦儒.开关电容DC/DC变换器的分析[J].电子学报,1997,25(2).
[4] 刘健,陈治明.开关电容DC/DC变换器的最佳控制方法[J].电子学报,1998,26(8).
[5] 刘健,陈治明,钟彦儒.开关电容DC/DC变换器的效率[J].微电子学1997,27(1).
[6] 刘健,陈治明,钟彦儒.逐压控制的开关电容DC/DC变换器[J].电力电子技术.1997,31(1).
