移相全桥ZVSDC/DC变换器的极点配置自适应预测控制
唐建军,梁冠安
(华南理工大学电力学院,广东 广州 510640)
1 引言
近年来,移相全桥ZVSPWMDC/DC变换器由于它的显著特点已经在中大功率场合得到广泛的应用。而通过采用模拟芯片UC3895调节其两桥臂间对应开关的导通相位差,可实现其PWM模拟控制。近年来随着微处理器价格不断下降和计算能力不断增强,采用数字控制已成为大中功率开关电源的发展趋势。移相全桥ZVSPWM变换器是一个脉动的非线性系统。非线性系统的数字控制是人们多年来研究的热门课题之一。为了实现其高控制性能,本文采用数字信号处理器(DSP)来控制上述变换器。首先建立移相全桥ZVSPWM变换器的准线性模型,然后在此模型的基础上应用极点配置自适应控制策略设计出数字控制系统。
2 移相全桥ZVSPWMDC/DC变换器的准线性模型
用状态空间平均法建立的DC/DC变换器线性小信号模型,描述系统在额定工作点附近的工作特性。然而,由于这种方法规定变换器的参数只能在额定工作点附近变化,因此,对于工作在各种参数变化较大(如输入电压变化较大)的移相全桥变换器来说,这种建模方法显然不是很有效。为了克服这一缺点,文献[2]提出了准线性建模方法。准线性模型由稳定点模型和该稳定点下的小信号扰动模型两部分组成。稳定点模型描述系统在特定输入电压和负载情况下的稳定特性,其稳定工作点是变化的;扰动模型描述变换器在稳定点的暂态特性,它不是围绕着固定工作点作扰动得出的小信号模型,而是围绕着变化的工作点作扰动,且其变量比前者减少的小信号差分状态方程来描述。
2.1 准线性小信号扰动模型
移相全桥ZVSPWMDC/DC变换器主拓扑如图1所示。如果以移相全桥变换器的输出电感电流IL,输出电容电压Vc,输入电压Vin和占空比D为变量,对这4个变量加小信号扰动,就能得出精确的线性小信号模型。这个模型可以精确地描述移相全桥变换器工作在固定工作点附近的特性。而建立其准线性小信号扰动模型时,不是对所有4个变量都施加扰动,若选择输入电压不作线性化扰动,则作线性化扰动的变量就只包括输出电感电流IL,输出电容电压Vc及占空比D,这样移相全桥变换器稳态工作点不再是固定的,而是随着输入电压的变化而变化,从而,上述变量小信号扰动的大小也应为变量瞬时值与其在相应的稳态工作点稳态值之差。图2是移相全桥变换器线性小信号电路模型[3],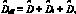 (
(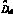 为有效占空比的总扰动量;
为有效占空比的总扰动量;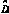 为滤波电感电流变化引起的
为滤波电感电流变化引起的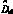 的变化量;
的变化量;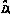 为输入电压变化而引起的
为输入电压变化而引起的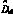 的变化量;
的变化量;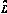 是原边占空比的变化量)。
是原边占空比的变化量)。
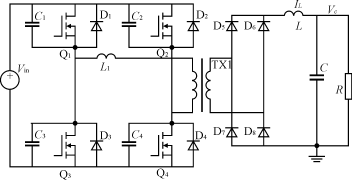
图1 移相全桥ZVS变换器的主电路
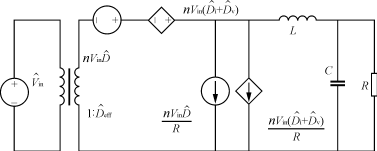
图2 移相全桥变换器的线性小信号电路模型
根据文献[3]建立线性小信号模型的方法,建立准线性小信号扰动模型,只要不考虑输入电压变化对有效占空比总扰动量的影响,就可得出其准线性小信号扰动模型,如图3所示。
根据图3可得出准线性小信号扰动模型的状态方程,即
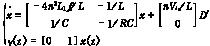 (1)
(1)
式中:x(t)为状态变量,包括小信号滤波电感电流和小信号滤波电容电压两个状态变量,分别等于输出电感电流和输出电压与它们的设定值之差;
D′为小信号占空比扰动输入;
y(t)为输出变量;
L为输出滤波电感量;
C为输出滤波电容量;
R为负载;
Vin为输入电压;
n为变压器副边与原边的匝数比;
L1为谐振电感;
fs为开关频率。
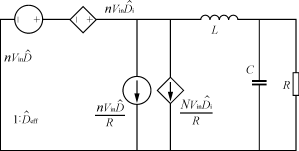
图3 移相全桥变换器的准线性小信号扰动模型
离散化后可得出其差分方程为
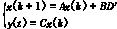 (2)
(2)
2.2 稳态工作点模型
通常,变换器的输出电感电流IL与输出电容电压Vc,随输入电压变化而变化,但在实际中,往往要求开关电源的输出电压维持在一个固定值。假设输出电容串联电阻很小,则输出电容电压就等于输出电压,这样,稳态工作点(Ucop,ILop,Dop)中的输出电容电压Ucop是一个常数,又由于变换器平均电感电流等于负载电流,因此,取其参考电感电流ILop等于负载电流,从而移相全桥变换器在稳定工作时的占空比,可表示为系统稳定点状态变量和系统输入电压的函数。移相全桥变换器工作过程中有占空比丢失的问题,有效占空比Deff为变压器次级占空比,Deff和丢失的占空比ΔD可分别表示为
Deff= (3)
(3)
ΔD=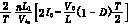 (4)
(4)
式中:T为开关周期。
于是控制用的原边占空比Dop可表示为有效占空比与丢失的占空比之和,即Dop为
Dop=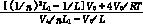 (5)
(5)
它是随着输入电压的变化而调整的,亦即此模型具有前馈控制的特点,对输入电压的扰动具有很强的抑制作用,能有效地保证了系统在大信号扰动下的稳定。
3 极点配置自适应数字控制
控制系统的动态响应是由系统的极点决定的。移相全桥变换器由于自身的非线性特点,使它的动态特性往往很差,并且可能造成系统的不稳定,因此,需要通过极点配置反馈作用使系统的极点配置到所希望的极点上,从而提高系统的动态特性和稳定度。控制方法是用状态变量IL和Uc同参考值比较所得的误差乘以反馈矩阵-l得到占空比的扰动值,即
D′=-lx l=〔l1-l2〕(6)
将式(6)代入式(2)得
x(k+1)=(A-lB)x(k)(7)
从而系统得特征方程为
det[ZI-A+lB]=0(8)
假设我们根据电源的动态要求,获得了所希望的极点为a1和a2,则系统希望的特征方程为
Z2-(a1+a2)Z+a1a2=0(9)
通过对比式(8)和式(9),状态反馈矩阵l很容易求出,这样就可以把极点配置到指定点上。但是,由于矩阵B是输入电压Vin的函数,相应的反馈矩阵系数l也是输入电压的函数,它会随着输入电压的变化而变化。因此,需要不断地根据输入电压的变化来调整反馈矩阵系数l,以满足要求的动态响应,这样就实现了自适应控制,从而提高了整个控制系统的控制性能。
4 控制算法的方框图及算法流程图
图4是用DSP实现移相全桥变换器数字控制的方框图。DSP的主要作用是根据输入电压,输出电感电流预测值IL′和输出电容电压预测值Vc′计算出变换器的占空比D,使全桥变换器的输出电压稳定在所要求的输出电压值。其计算方程式为
D=Dop+[-l1 -l2]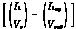 (10)
(10)
式(10)概括了本文所提出的基本控制思想。由于上述预测估算是每2个采样周期更新一次控制量,因此占空比也是每2个周期更新一次。
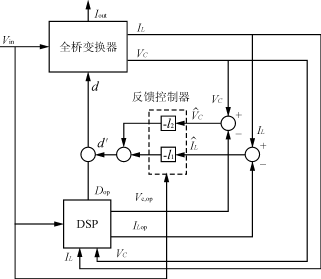
图4 控制系统方框图
驱动信号算法流程图如图5所示,从这里可看出根据准线性模型算出的占空比Dop是变化的,它决定了移相全桥变换器工作点的变化轨迹,且控制算法能根据变换器的动态变化不断调整系统的反馈矩阵系数l,以达到控制系统所要求的动态响应。
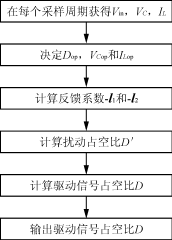
图5 算法流程图
5 Matlab仿真结果
设定移相全桥变换器的各项仿真参数如下:
变压器副边与原边的匝数比n=1∶3;谐振电感L1=17μH;滤波电容C=470μF;滤波电感L=360μH;开关频率fs=100kHz;Rd=4n2Lrfs;开关周期Ts=10μs;输出电压为U=50V。在这里设置希望配置的极点(Z域)为0.4+0.5j和0.4-0.5j,但它不一定是最优化的极点。
为了测试这种控制策略的有效性,进行以下仿真。
1)在设定初始占空比D=0.28时,系统从初始
零状态到稳态时的输出电压仿真波形,如图6所示。
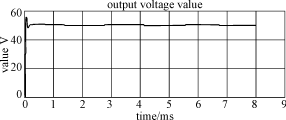
图6 初始状态到稳态过程的输出电压仿真波形
从图6中可以看出控制系统经过大约200μs就能达到稳定,超调量为6V,控制系统得动态响应较快。
2)当输入电压由220V突变为180V时,输出电压变化的仿真波形,如图7所示。从图7中可以看出,控制系统在输入电压突变时,从一个稳定状态调整到另一个稳定状态需要大约3ms,输出电压的波动很小,最大为0.12V。
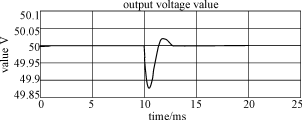
图7 输入电压突变时输出电压变化过程的仿真波形
3)当负载由5Ω突变为10Ω时,输出电压变化的仿真波形,如图8所示。从图8中同样可以看出,控制系统在输出负载突变时,从一个稳定状态调整到另一个稳定状态需要大约3ms,且输出电压的波动很小,大约为0.2V。
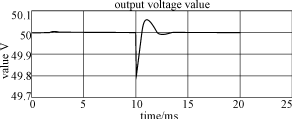
图8 负载突变时输出电压变化过程的仿真波形
从以上仿真波形可以看出,使用以上控制算法可使移相全桥变换器有较好的动态响应和稳定性,并且控制算法简单,易于实现。
6 结语
本文介绍了移相全桥变换器采用准线性建模和极点配置自适应数字控制的控制思想。准线性模型可以很好地描述系统在大扰动下的工作特性,极点配置自适应数字控制综合了自适应控制和极点配置控制两者的优点,通过仿真证明了这种控制策略不但算法简单,实现容易,并且可以保证变换器在各稳定工作点都有很好的动态特性和稳定性。另外这种控制策略可以用TI公司的DSP作为主控芯片来实现其数字控制,使得控制系统有更高的稳定性、可靠性和更强的灵活性。
