基于DSP的矩阵变换器空间矢量控制
王勇,吕征宇,汪槱生
(浙江大学电力电子国家专业实验室,浙江 杭州 310027)
1 引言
矩阵式变换器是一种具有优良的输入输出特性的新型交—交变换器。它允许频率单级变换,无需大容量的贮能元件如大电容,可使输入电流正弦,输入功率因数达到0.99以上,并可自由调节,且与负载的功率因数无关,输出电压正弦,输出频率及电压可调,输出频率可高于、低于输入频率,特别是其功率可双向流动,具有四象限运行能力。本文在矩阵变换器的空间矢量控制基础上,给出了一种基与DSP+PLD的方案,实验证明此方案可以提高高频大电流下换流的可靠性,简化了控制系统。
2 矩阵式变换器的空间矢量调制
一个用于实现交—交变换的矩阵式变换器如图1所示。它可以用一个虚拟的整流器和一个虚拟的逆变器构成的等效交—直—交结构来代替,如图2所示。采用这样的等效结构可以充分利用已有成熟的交—直—交变换中的PWM控制技术,并可通过开关函数分析出实际矩阵式变换器的开关控制规律。
分析图1和图2时,首先要定义开关函数。
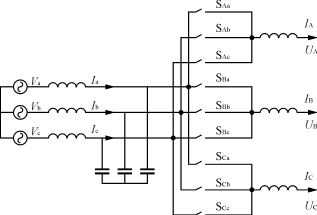
图1 矩阵变换器结构
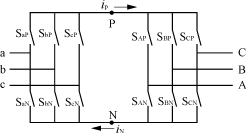
图2 等效交—直—交结构
对于图2的等效交—直—交结构,j∈{a,b,c,A,B,C,},k∈{P,N}。按照输入电压不能被短路,输出电路不能突然开路的原则,虚拟整流器同一直流母线P或N上的开关必须有一个且只能有一个处于导通状态,即
Sak+Sbk+Sck=1,k∈{P,N} (1)
而虚拟逆变器同一输出相A,B或C上必须有一个而且只能有一个开关导通,即
SjP+SjN=1,j∈{A,B,C,} (2)
对于图1的矩阵式变换器实际结构,j∈{A,B,C,},k∈{a,b,c}。按照输入电压不能被短路,输出电路不能突然开路的原则,每一输出相只能连至且必须连至一个输入相,开关函数须满足
Sja+Sjb+Sjc=1,j∈{A,B,C,} (3)
能满足式(3)的开关组合共有27种,但有6种在等效交—直—交结构中找不到对应的开关组合,所以共有21种有效的开关组合和矢量,见表1。
表1 矩阵式变换器有效开关组合表及与等效交—直—交变换器对应关系
| 21种有效矢量开关组合
| 开关状态
S SAbSAcSBaSBb
SBcSCaSCbSCc
| 输出电压
| 输入电流
|
| UAB
| UBC
| UCA
| Ia
| Ib
| Ic
|
| 1P
| 100 010 010
| Uab
| 0
| -Uab
| IA
| -IA
| 0
|
| 1N
| 010 100 100
| -Uab
| 0
| Uab
| -IA
| IA
| 0
|
| 2P
| 010 001 001
| Ubc
| 0
| -Ubc
| 0
| IA
| -IA
|
| 2N
| 001 010 010
| -Ubc
| 0
| Ubc
| 0
| -IA
| -IA
|
| 3P
| 001 100 100
| Uca
| 0
| -Uca
| -IA
| 0
| IA
|
| 3N
| 100 001 001
| -Uca
| 0
| Uca
| IA
| 0
| -IA
|
| 4P
| 010 100 010
| -Uab
| Uab
| 0
| IB
| -IB
| 0
|
| 4N
| 100 010 100
| Uab
| -Uab
| 0
| -IB
| IB
| 0
|
| 5P
| 001 010 001
| -Ubc
| Ubc
| 0
| IA
| IA
| IC
|
| 5N
| 010 001 010
| Ubc
| -Ubc
| 0
| 0
| -IB
| IB
|
| 6P
| 100 001 100
| -Uca
| Uca
| 0
| IB
| IC
| IA
|
| 6N
| 001 100 001
| Uca
| -Uca
| 0
| IB
| 0
| -IB
|
| 7P
| 010 010 100
| 0
| -Uab
| Uab
| IA
| -IA
| 0
|
| 7N
| 100 100 010
| 0
| Uab
| -Uab
| -IA
| IC
| 0
|
| 8P
| 001 001 010
| 0
| -Ubc
| Ubc
| 0
| IC
| -IC
|
| 8N
| 010 010 001
| 0
| Ubc
| -Ubc
| 0
| -IC
| IC
|
| 9P
| 100 100 001
| 0
| -Uca
| Uca
| -IC
| 0
| IC
|
| 9N
| 001 001 100
| 0
| Uca
| -Uca
| IC
| 0
| -IC
|
| 0A
| 100 100 100
| 0
| 0
| 0
| 0
| 0
| 0
|
| 0B
| 010 010 010
| 0
| 0
| 0
| 0
| 0
| 0
|
| 0C
| 001 001 001
| 0
| 0
| 0
| 0
| 0
| 0 |
经过推导可得到等效交—直—交结构和矩阵变换器的开关函数关系为
Sjk=SjPSkP+SjNSkN, j∈{A,B,C,},k∈{a,b,c} (4)
限定条件为
1≤SGm+SJn+SKI≤2 (5)
式中:G,J,K∈{A,B,C,},m,n,1∈{a,b,c},且G≠J≠K,m≠n≠1。
根据式(4)可以得到矩阵变换器21种有效开关组合形成的矢量与等效交—直—交结构6个输入相电流矢量和6个输出线电压矢量的对应关系,见图3和表1,从而由等效交—直—交结构的双空间矢量调制策略得到矩阵变换器的交—交直接变换空间矢量调制策略。
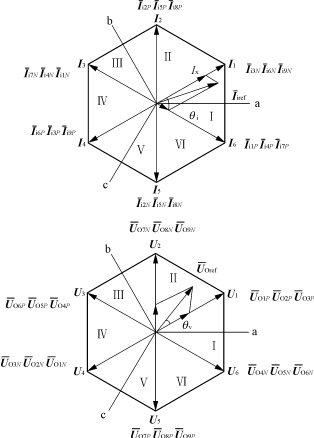
图3 输入相电流和输出线电压的矢量图
在等效交—直—交结构中,逆变器部分的理想输出线电压基准矢量圆和整流器部分的理想输入相电流基准矢量圆都被划分为6个扇区,从而有36种可能的扇区组合,以虚拟整流器、逆变器均工作在第I扇区为例,可以用于矢量合成的空间电流,电压矢量分别是I6,I1和U6,U1,两个空间矢量的综合调制采用相互嵌套的办法来实现。整个输入相电流和输出线电压矢量合成过程共有I6-U6,I6-U1,I1-U6,I1-U1及零矢量I0-U05种组合。每一矢量组合的作用时间用占空比表示时是该组合内各矢量占空比的乘积。即
I6-U6:
Dxα=Dx·Dα=msin(60°-θi)sin(60°-θv) (6)
I6—U1:
Dxβ=Dx·Dβ=msin(60°-θi)sinθv (7)
I1-U6:
Dyα=Dy·Dα=msinθisin(60°-θv) (8)
I1-U1:
Dyβ=Dy·Dβ=msinθisinθv (9)
I0-U0:
D0=1-Dxα-Dxβ-Dyα-Dyβ (10)
式中:θi是输入相电流的相角;
θv是输出线电压的相角。
以上计算出占空比后,再通过开关函数找到相对应的真实的矩阵变换器的矢量和开关组合。开关组合的选择步骤、原则如下:假设输出线电压矢量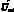 和输入相电流
和输入相电流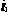 都位于第1扇区,则根据图3得到合成
都位于第1扇区,则根据图3得到合成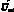 和
和 的固定矢量U1,U6,I1,I6,并得到对应的矩阵变换器的8个矢量1P,3P,4P,6P,1N,3N,4N,6N,再按照获得最大电压传输比和单位功率因数的原则从上述8个矢量中选出4个矢量。要获得单位功率因数,则要使输入相电压和输入相电流相角差为0,注意到输入线电压矢量超前输入相电流30°,则输入线电压矢量可能位于第1扇区或第2扇区,所以,输入线电压的最大值为Uab和-Uca,则在上述8个矢量中需要选择4个矢量使输出线电压UOAB等于Uab或-Uca,选出的4个矢量为1P,3N,4N,6P,4个矢量按照开关次数最少的原则确定开关顺序为1P,3N,4N,6P,加上零矢量,5个矢量的占空比由式(6),(7),(8),(9),(10)确定。输出线电压矢量
的固定矢量U1,U6,I1,I6,并得到对应的矩阵变换器的8个矢量1P,3P,4P,6P,1N,3N,4N,6N,再按照获得最大电压传输比和单位功率因数的原则从上述8个矢量中选出4个矢量。要获得单位功率因数,则要使输入相电压和输入相电流相角差为0,注意到输入线电压矢量超前输入相电流30°,则输入线电压矢量可能位于第1扇区或第2扇区,所以,输入线电压的最大值为Uab和-Uca,则在上述8个矢量中需要选择4个矢量使输出线电压UOAB等于Uab或-Uca,选出的4个矢量为1P,3N,4N,6P,4个矢量按照开关次数最少的原则确定开关顺序为1P,3N,4N,6P,加上零矢量,5个矢量的占空比由式(6),(7),(8),(9),(10)确定。输出线电压矢量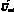 和输入相电流
和输入相电流 共有36种扇区组合,则对应矩阵变换的36种矢量调制开关组合。
共有36种扇区组合,则对应矩阵变换的36种矢量调制开关组合。
3 安全换流策略
本系统采用共集电极的反向串联IGBT组合开关组成双向功率开关,根据输入电压不能被短路,输出电路不能突然开路的条件,安全切换要求同一相输出的任意两组开关不能同时导通,三组开关不能同时断开。由于器件的开通时间,关断时间,及驱动电路的时延都有差异,不能做到严格的同时切换。为了解决这个问题,N.Burany提出了著名的四象限开关多步切换控制法,其换流过程可用图4及图5所示一相输出电路来说明。以由a输入相换流到b输入相为例,当负载电流iL>0时,第1步关断负导通部分SlN,第2步开通S2P,第3步关断S1P,第4步开通S2N,以此完成两个双向开关的成功换流,既禁止了可能使电源发生短路的开关组合,又保证了在任意时刻给负载提供至少一条流通路径。
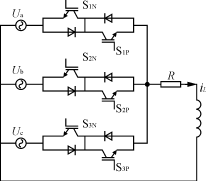
图4 一相输出电路示意图
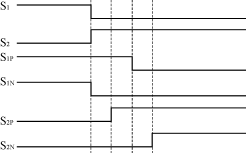
图5 4步换流策略驱动信号示意图
4 控制系统设计及实验结果
图6是以DSP为控制核心的矩阵变换器系统框图,DSP检测输入相电压的扇区,得到期望的输出线电压扇区后,通过空间矢量调制策略,DSP送出6路驱动信号及保护信号到PLD,四步换流,驱动等逻辑由模块内部逻辑器件PLD完成,PLD送出18路驱动信号到主电路的18个分立开关。
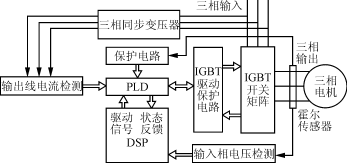
图6 矩阵变换器实验系统框图
波形如图7,8,9,采样频率为10kHz,调制比M=0.866,输入滤波器参数:L=30mH,C=15μF。
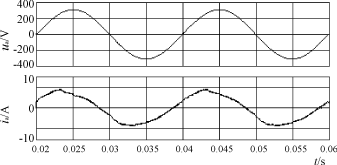
图7 输入相电压ua波形与输入相电流ia波形
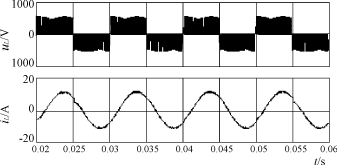
图8 输出线电压uL与输出线电流iL波形
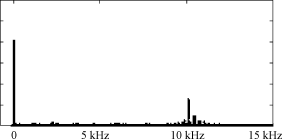
(a) 输入相电流
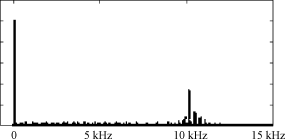
(b) 输出线电压
图9 FET分析
5 结语
以DSP+PLD构成的矩阵变换器控制系统结构简单,系统接线少,控制电路与软件简单,很好地解决了矩阵变换器的关键问题——安全换流,大大提高了高频大电流下顺序换流的可靠性,系统可靠性得到提高,为矩阵变换器向大功率,数字化发展和工业应用奠定了基础。
