三相PWM整流器全解耦方式研究

卢至锋，张波

(华南理工大学电力学院，广东    广州    510640）

1    引言

    现在，三相功率因数校正技术已成为电力电子技术研究的一个热点。三相PFC整流装置具有输入功率高，三相输入功率脉动部分的总和为零，输出电容无工频纹波等优点。但是，三相PFC整流电路有一个很大的难题就是三相之间存在耦合。近年来，有不少关于三相PFC的解耦电路被提出，主要分为部分解耦PFC和全解耦三相PFC二大类。

    本文着重于全解耦三相PFC电路，并对各种全解耦三相PFC的解耦方式，控制方式和调制方式，进行了比较，分析和研究。

2    三相PWM整流器全解耦和控制方式分析

2.1    三相隔离全解耦

    三相隔离全解耦PFC是一种最基本的全解耦PFC，输入端有个全波整流器，跟着是一个串联谐振电路，电压被谐振电容箝位,其电路如图1所示。电路的开关频率很高，在谐振整流器的一个开关周期内，输入电压v_in被认为是一个常数。

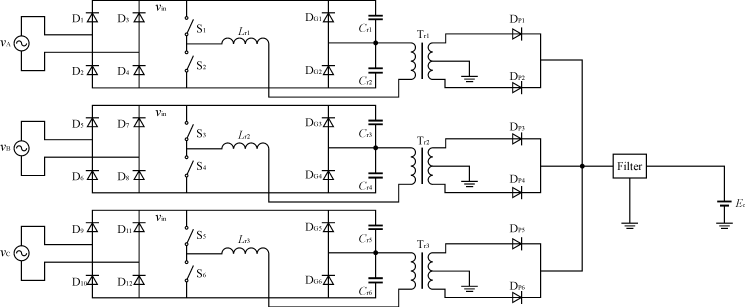
图1    三相隔离全解耦PFC电路

    A相工作原理如下：在一个开关周期内，有2个谐振阶段和2个二极管续流阶段，上下桥臂驱动信号互补。图2为开关管和谐振电容电压波形。

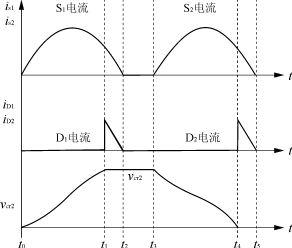
图2    上下桥臂开关管电流和谐振电容电压波形

    阶段1（t₀－t₁）谐振    初始状态为i_Lr1=0；v_cr1=v_in；v_cr2=0。S₁，D₁，D₄导通，i_Lr1，v_cr1和v_cr2正弦变化，当v_cr2=v_in时，二极管D_G1是正向偏压。

    阶段2（t₁－t₂）    线性初始状态为i_Lr1=I₁；v_cr3=v_in；v_cr1=0，I₁为最大电流。S₁，D₁，D₄，D_G1导通，电流i_Lr1线性减少到0，电压v_cr1和v_cr2保持不变。

    阶段3（t₂－t₃）    稳态v_cr3=v_in，i_Lr1=0

    阶段4（t₃－t₄）    谐振初始状态为i_Lr1=0；v_cr1=0；v_cr2=v_in。S₂，D₂，D₃导通，i_Lr1，v_cr1和v_cr2正弦变化，当v_cr1=v_in时，二极管D_G2是正向偏压。

    阶段5（t₄－t₅）    线性初始状态为i_Lr1=－I₁；v_cr1=v_in；v_cr2=0。S₂，D₂，D₃，D_G2导通，电流i_Lr1线性减少到0，电压v_cr1和v_cr2保持不变。瞬态平均输入电流I_inAV为

    I_inAV=f_sV_in/ω₀Z₀    （1）

式中：ω₀为1/；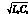

      C_r为C_r1＋C_r2；

      L_r1=L_r2=L_r3=L_r；

      Z₀=；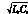

      f_s为开关频率。

    这种拓扑每相的整流器是独立的，实现了三相全解耦，驱动电路简单而容易实现，三极管S1和S2的关断很自然地进行，表现出零电流开关变流器的特性，但明显存在开关器件多，电路不紧凑和均流问题。

2.2    基于非线性反馈控制策略的三相解耦

    主电路采用三相CCM-Boost整流电路，在建立同步旋转坐标系下的三相电压型PWM整流器模型的基础上，基于非线性系统反馈线性化理论，提出了一种非线性控制策略，从而实现全解耦PFC。

    同步旋转坐标系下的三相电压型PWM整流器模型为^[3]：

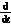    i_sd=ωi_sq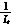－v_sd－v_dcm_vd    （2）

    i_sq=－ωi_sd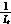－v_sq－v_dcm_vq    （3）

    v_dc=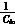(m_vdi_sd＋m_vqi_sq)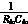－v_dc    （4）

式中：m_vd，m_vq为同步旋转坐标系下的开关函数量；

      v_dc为直流侧电容电压；

      C_dc，R_dc分别为直流侧电容，电阻。

    根据非线性反馈线性化理论，选择非线性坐标变换z₁=i_sd，z₂=i_sq引入非线性状态反馈u_vd和u_vq，可以求出以下模型

    =－kz₁＋ku_vd    （5）

    =－kz₂＋ku_vq    （6）

式中：ku_vd=ki_sd＋ωi_sq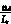＋－v_dcm_vd；（7）

      ku_vq=－ωi_sd＋ki_sq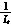＋－v_dcm_vq。（8）

电源有功（p_s）和无功（q_s）定义如下

    p_s=v_sdi_sd，q_s=－v_sdi_sq    （9）

    从式（9）可以看出，无功q_s可以通过调制无功电流i_sq来实现直接控制。整流器的无功和有功可以独立控制，并实现了三相完全解耦，但是控制非常复杂。

2.3    空间矢量控制解耦

    空间矢量控制主要应用于三相CCM-Boost整流电路，如图3所示。

图3    三相CCM-Boost整流电路

    三相正弦输入电压为v_A，v_B，v_C，且v_A＋v_B＋v_C=0，在旋转坐标系下，定义空间矢量变换式

    v=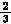(v_A＋v_B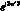＋v_C)    (10)

    三相变流器的不同开关模式形成6个非零电压矢量和2个零电压矢量（见图4），如果用变流器6个非零电压矢量和2个零电压矢量去逼近矢量圆，则变流器输入端会得到等效的三相正弦波形，实现三相输入电压完全解耦。

图4    矢量与矢量合成

    如图4所示，设采样周期为T_s，则任一空间矢量可由其相邻的2个开关矢量来等效，相应导通时间为

    t_α=mT_ssin(π/3－θ_r)    （11）

    t_β=mT_ssinθ_r    （12）

式中：m为调制比，m=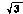v_r/v_dc（vr为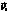的模）

    零矢量作用的时间t₀=T_s－t_α－t_β    （13）

    空间矢量控制能够有效地消除低次谐波和全解耦，控制比非线性反馈控制简单，易于实现。

3    试验

    本文采用TMS320F2407作为系统控制的核心，采用空间矢量解耦方式，电压有效值50V，电源频率50Hz，电路输入电感L_A=L_B=L_C=10mH，C_dc=200μF，R_dc=20Ω，开关频率900Hz，系统框图如图5所示。图6为A相输入电压与输入电流波形。

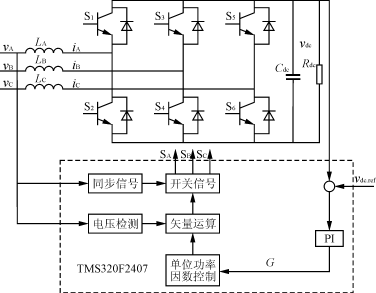
图5    系统框图

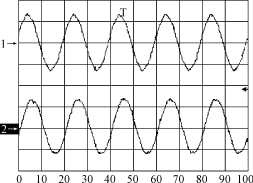
图6    A相输入电压（上：50V/格）与输入电流（下：10A/格）

    从图6可以看出，电流波形跟随电压波形，功率因数接近为1。

4    结语

    1）以上3种解耦方式都能够实现三相完全解耦。

    2）从主电路结构，解耦控制等几个方面比较，空间矢量控制解耦为最优全解耦方式。