数字控制中控制延时的影响及改进PI消除饱和积分的探讨

王晓薇1，程永华2

(1�闭憬�大学信息学院，浙江    杭州    310027）

(2�鄙虾Ｌù锏缌Φ缱友蟹⒅行模�上海    201209）  

1    引言

    传统的电源都是采用模拟控制，模拟控制经过多年的发展，已经非常成熟。然而，模拟控制有着固有的缺点，诸如：元器件数量多，连接复杂，使系统的故障检测与维修比较困难；器件的老化和温漂，易受环境（如电磁噪声，工作环境温度等）干扰，从而影响系统的长期稳定性；控制不够灵活，不易实现复杂、先进的控制算法。

    数字控制电源是当今电源发展的方向，与传统模拟控制相比，数字控制可以简化硬件电路，消除模拟电路固有的温漂问题，提高控制精度，易实现先进控制，且降低了电路成本，易实现大规模产品生产。高速微处理器如DSP（Digital Signal Processing数字信号处理器）的出现，使得数字控制技术实时性迅速提高，从而得到了更广泛的应用。然而，在数字控制系统设计中要注意以下几个问题^[1]：A/D转换的精度和速度，采样频率的选取，PWM频率及其精度，控制算法的延时，字长效应，计算精度以及数字控制算法的优化等。本文以基于DSPTMS320F240控制的逆变电源为例，着重探讨了数字控制中控制延时对系统的影响以及使用改进数字PI消除积分饱和现象等问题。

2    数字系统构成

    图1为数字控制的电源系统的典型结构框图。系统包括模拟部分、数字部分以及模拟数字的接口电路。模拟部分主要是各种拓扑的变换电路及负载电路。数字部分为微处理器芯片及其外设。接口电路包括从模拟部分到数字部分的采样网络及A/D转换器和从数字部分到模拟部分的PWM口外围电路、相应的门极驱动电路及D/A转换器或IO口外围电路。

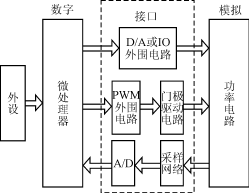
图1    数字控制的电源系统的典型结构框图

    在基于DSP TMS320F240控制的逆变电源中，采用了外环平均值环、内环瞬时值环的双环控制策略。内环通过瞬时值控制获得快速的动态性能，保证输出畸变率较低，外环使用输出电压的平均值控制，具有较高的输出精度。通过DSP内部A/D采样一个周期的输出电压值可以计算出输出电压的有效值，和设定的输出电压值比较，误差信号通过外环数字PI调节器运算，得到的外环输出乘以单位幅值正弦波作为内环给定信号。内环给定信号与A/D采样得到输出电压瞬时值比较，其误差信号经内环数字PI调节器运算，得到了内环的控制信号，最后送入PWM调制器控制PWM脉冲的产生^[2]。

    在数字控制中，A/D转换器不可避免地存在量化误差，而这种量化误差对系统来说是一个不利影响。选择高精度的A/D转换器无疑能提高系统的控制精度，但是，也同时增加了系统的成本。根据采样定理，信号的采样频率至少为被控电路系统带宽的2倍，才不会出现混叠效应。提高采样频率能提高控制系统的实时性，但是，这通常受到A/D采样芯片的速度及微处理器速度的限制。PWM信号频率和精度对控制系统的精度影响最大，一般来说，开关频率越高，控制间隔越小，精度也就越高，但同时开关损耗也就越大。另外，在微处理器中，PWM频率和数字控制所特有的量化误差对PWM精度影响却是矛盾的，如对于DSPTMS320F240而言^[3]，系统的时钟频率为20MHz，当PWM频率为20kHz时，定时器的置数为1000，PWM量化误差为1％，而当PWM频率为时50kHz，定时器的置数为400，PWM量化误差为2.5％。字长效应及计算精度也是影响系统控制精度指标一个重要因素。在运算过程中，数据最初来自A/D转换器，A/D转换器的位数即采样的分辨率，首先影响后面计算所能得到的最大精度。在数据处理过程中，在保证无溢出的情况下，使得数据的字长最大，这样可以减小量化误差带来的影响，另外，在需要截尾时，通过舍入法即按最近的值取N位，使得误差对称分布，避免单纯截尾所带来误差单极性分布，减小对系统精度的影响。

3    控制延时分析

    在逆变电源数字控制系统中，由于A/D采样时间以及运算时间，使得当前周期计算所得到的脉宽只能在下个周期才能使用，这样，在控制上要延迟一个开关周期。在连续s域中，延时环节可以用G_o(s)=（t_d为延时时间）环节来表示。在离散z域中，可以用G_o(z)=z^－1环节来表示。G_o(s)=的波特图如图2所示。

图2    延迟环节G_o(s)=的波特图

    从图2可以看出，G_o(s)在整个频域段中，其增益20lg A≡0，也即A≡1，对系统的增益不产生影响。而其相角随着角频率增加而减小，延时环节的存在使得所设计的系统的相角裕度变小。如果所设计的系统的穿越频率为ω_o rad/s，而延迟环节的时间常数为T_s，则系统将损失的相角裕度为360°×。

    考虑控制延时后逆变电源系统的控制框图如图3所示。

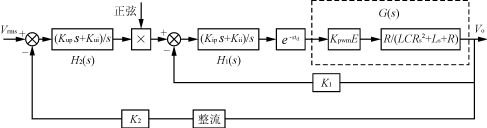
图3    考虑延时环节后系统的控制框图

    不考虑延时环节，内环开环传递函数的相角随频率变化曲线如图4曲线1所示。选择电源的开关频率为20kHz，则控制上要延时50μs，延时环节G(s)=，可以得到考虑延时环节后，内环开环传递函数的相角随频率变化曲线如图4曲线2所示。选择逆变电源内环开环传递函数的穿越频率为ω_o=6280rad/s，则延时环节的存在使得系统损失的相角裕度为18°。

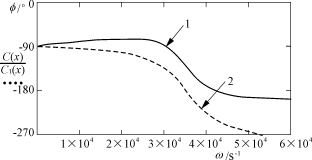
1——无延时环节内环补偿后开环相角曲线

2----有延时环节内环补偿后开环相角曲线

图4    考虑延时环节和不考虑延时环节补偿后内环开环传递函数的相角变化曲线

    从上面分析知，延迟环节的存在使得系统的相角裕度减小，导致系统抗干扰能力下降，严重时可能使得系统不稳定。

4    改进PI算法

    从模拟校正器转换为数字校正器的方法主要有3种：冲击响应不变法，阶跃响应不变法，双线性变化法。

    以冲击响应不变法为例，设PI调节器的输出量为u(t)，输入量为e(t)，调节器的比例系数为K_p，积分时间常数为T_i，则PI调节器的传递函数为

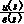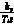    =K_p＋    （1）

写成时域方程，再离散化，采样增量式算法可以得到PI控制算法的数字化方程^[4]为

    y_k=y_k－1＋(K_p＋K_pK_I)e_k－K_pe_k－1    （2）

式中：y_k为PI调节器的第k次输出值；

      y_k－1为PI调节器的第k－1次输出值；

      e_k为第k次采样时，给定量和反馈量之间的差值；

      e_k－1为第k－1次采样时，给定量和反馈量之间的差值；

      K_I为积分系数，K_I=T_s/T_i，T_s为PI调节器的采样周期。

    数字控制中，数字PI的输出变量必须被限制在一个有限范围内。对于时间常数较大的控制环节，系统的偏差通常不会在几个采样周期内消除掉，如采用标准的数字PID算法，积分项会使得PI输出在较长的时间内处在上下极限值，这样输出值就会超出正常范围，出现较大的超调。这种现象称为积分饱和，如图5所示。曲线b对应为系统输出，当输出到达设定值r时，由于积分作用，使得PI的输出（曲线a）在后面的t₀时间内继续保持在饱和位置，这样就造成输出出现较大的超调，且可能出现振荡。

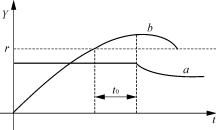
图5    PID算法积分饱和现象

    克服饱和积分可以采用以下方法^[5]。

    1）过限削弱积分法    一旦控制变量进入饱和区，则程序只执行削弱积分项的运算，而停止增大积分项的运算。

    2）积分分离法    积分分离法基本思想为：当误差e大于某个规定的门限值时，删去积分作用，从而使得积分项不会累计过大，只有当误差e较小时才引入积分作用，以消除稳态误差。

    逆变电源的外环为平均值环，时间常数较大，采用过限削弱积分法，使得外环输出较易退出饱和。外环的控制框图如图6所示。

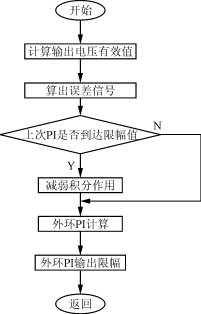
图6    外环程序的控制框图

5    实验结果

    实验结果如图7所示。图7（a）为外环使用普通数字PI算法，逆变电源的软启动电压波形。图7（b）为使用改进的数字PI算法，逆变电源的软启动电压波形。从图7可以看到，使用改进数字PI算法后，缩短了启动时间，减小了软启动的超调量，改善了逆变电源的启动性能。

（a）普通数字PI算法电源的软启动电压波形

t:500ms/格    u:200V/格

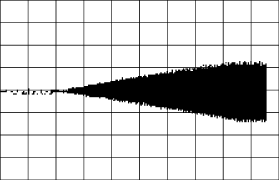
（b）改进数字PI算法电源的软启动电压波形

t:500ms/格    u:200V/格

图7    软启动电压波形对比图

6    结语

    本文讨论了数字控制中所要注意的一些问题，并以基于DSP TMS320F240控制的逆变电源系统为例，着重探讨了数字控制中控制延时对系统的影响以及使用改进数字PI消除积分饱和现象等问题。延迟环节的存在使得系统的相角裕度减小，导致系统抗干扰能力下降，严重时可能使得系统不稳定。使用改进数字PI算法可以使时间常数较大的控制环节较易退出饱和，减小超调量，加快响应速度。