1.概述

软开关技术、谐振型开关变换技术使得大功率、高频化电源的实现成为可能，它应用谐振的原理，使开关器件中的电流(或电压)按正弦或准正弦规律变化采用软开关技术，其实质就是在主开关上增加电感和电容等储能元件构成谐振电路.当变换器主开关进行换流时产生谐振，迫使主开关上的电压或电流变为零，从而为主开关提供一个零电压或零电流的开关环境。最理想的软开通过程:电压先下降到零后，开通主管，电流上升到通态值，开通损耗近似为零。另外，因器件开通前电压已下降到零，器件结电容上的电压亦为零，故解决了容性开通问题.这意味着二极管已经截止，其反向恢复过程结束，因此二极管反向恢复问题亦不复存在.最理想的软关断过程:电流先下降为零开通主管电压上升到断态值，所以关断损耗近似为零.由于器件关断前电流已下降到零，即线路电感中电流为零，所以感性关断问题得以解决。它不仅可以解决硬开关变换器中的硬开关损耗问题、容性开通问题、感性关断问题及二极管反向恢复问题，而且还能解决由硬开关引起的EMI等问题。本课题研究的电源功率为32kW，工作频率为5kHz~20kHz,为了减小高频时开关器件的损耗，采用串联谐振软开关技术，使得开关器件能够实现零电流关断，其主电路原理图如图 1所示：

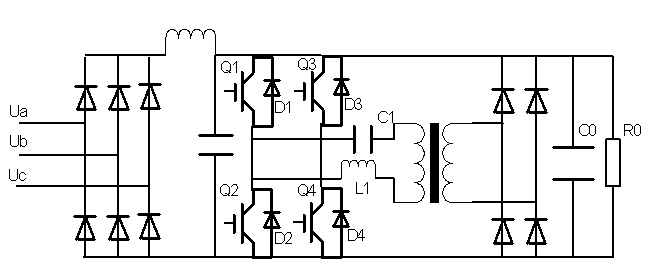
图1 全桥串联谐振式电路原理图

2.原理分析

该电路有三种工作模式：

(1).         谐振电感电流断续工作，开关管为零电流导通，零电流/零电压关断，反并二极管为自然开通和关断。

(2).             ，谐振电感电流连续工作，开关管为零电压/零电流关断，但开通是硬开通，存在开通损耗。

(3).          谐振电感电流连续工作，开关管为零电压/零电流开通，但关断是硬关断，存在关断损耗。

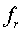
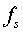
其中     —开关频率，   —谐振频率

为了减小开关损耗，在电路工作中，使得开关频率小于或等于谐振频率的一半，使电流工作在断续状态。结合上面的分析，我们对图 1电源主回路等效原理图的工作模态进行计算分析。

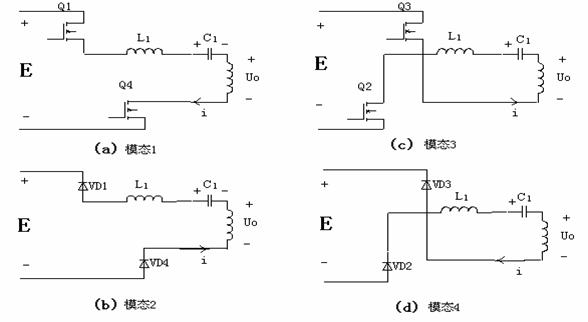
图2 等效电路模型

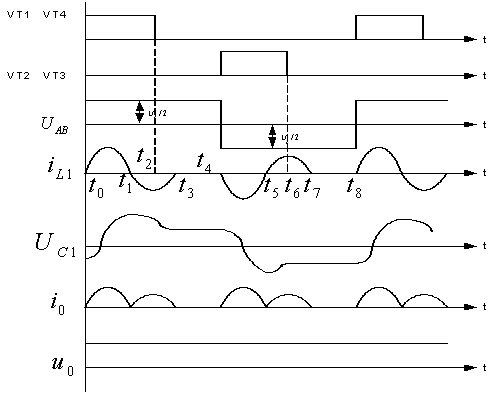
图 3  电流断续工作方式的主要波形

设电感L₁电流为i，电容C₁电压为U₁，电源一个谐振周期内各个模态图如图4所示，电源工作波形如图 3所示。电路工作特点是：开关频率fs必须低于谐振频率fr的一半，保持主回路串联谐振条件恒定不变，使整个电路工作于不连续导电模式。对于主电路中的逆变电路，采用脉冲频率调制（PFM）改变开关频率，驱动脉冲满足：在正常的导通情况下，加在逆变开关上的驱动信号应该是互补的，即当第一组(VD1与VD4)开管导通时，第二组开关(VD2与VD3)截止；第二组开通时，第一组截止。电路具体工作流程分析如下：首先假定输入的滤波电容的容量足够大，在逆变过程中其上的电压E基本保持不变，由于储能电容远大于谐振电容，可以把每一个开关周期看成是恒压源电压不断上升的过程。这样可以将图1中的电路的工作过程等效为4个工作模态，其中U₀=Uco/K，Uco为负载电压，K为高频变压器的变比。以图2（a）中电流方向为正，则等效电路满足2-1和2-2式：

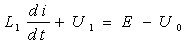
                                (2-1)

                                   (2-2)

式中：U₁为谐振电容C₁两端电压；U₀为负载电容C₀的电压这算到变压器原边的电压。

模态1的等效电路如图2（a）所示，考虑初始状态时U₀(t0)=0，U₁(t₀)=0，i(t₀)=0利用回路电流法可以求出谐振回路的谐振电感电流和谐振电容电压（电路工作在电流断续状态fs＜0.5fr）：

                                             （2-3）

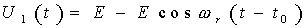                                                     （2-4）

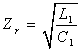
其中，              为谐振角频率，fr为谐振频率；          为特征阻抗。t₀时刻

开通Q1、Q4，电流i正向移动，L₁与C₁谐振，到t₁时刻i过零，U₁达到最大值，电路进入第二模态。

模态2的等效电路如图2（b）所示，电流i反向，流过功率管Q1、Q4的体二极管VD1、VD4，且数值逐渐增大，U₁逐渐减少，t₂时刻关断Q1、Q4，由于此时VD1、VD4导通，故Q1、Q4属零电流关断。模态2的初始条件为i(t₁)=0，U₁(t₁)=2E，U₀(t₁)大于零。其中，U₀是模态1结束后负载电容C₀上的电压值折算到变压器原边的数值。电路方程：

                                                     （2-5）

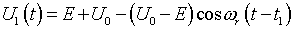                                                   （2-6）

t₃时刻i1到零，VD1、VD4自然关断，模态2结束。

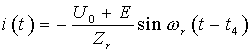t₄时刻开通Q2、Q3，电流i谐振增加，变化率平缓，实现Q2、Q3软开通，电路进入第3模态，开始又一个谐振周期。第3模态的等效电路如图2（c）所示，模态3的初始值为i(t₄)=0，U1(t₄)=2U₀(t₄)，U₀(t₄)=U₀(t₃)。电路方程：

                                                        （2-7）

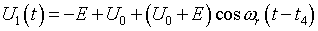                                                        （2-8）

t₅时刻i到零，VD2、VD3导通，电路第3模态结束。

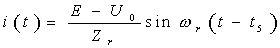模态4的等效电路如图2（d）所示，初始条件为i(t₅)=0，U₁(t₅)= -2E，U₀(t₅)＞U₀(t₄)。电路方程：

                                                        （2-9）

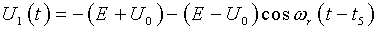           （2-10）

t₆时刻i到零，Q2、Q3零电流关断。t₇时刻VD2、VD3自然关断，模态4结束。

分析4个模态的方程，可以看出电流i峰值的变化规律，   Im(1)=E/Zr，     Im(3)=︱-(E+ U₀)/Zr︱，与Im(1)相比，Im(3)有所增加。Im(2)=︱(U₀-E)/Zr︱，Im(4)= ︱(E- U₀)/Zr︱，后式中U₀的值比前式的大，因此，与Im(2)相比，Im(4)有所减少。若列出下一个谐振周期的电路方程，同样有此规律。这样随着谐振次数的增加，储能电容上的电压也随之增加到设定值。

从上面的推导可以看出：

①输出电流的幅值在输入电压E和谐振参数一定时，仅与负载电容折算到原边的电压值有关，而在一个谐振周期内的电流有效值是不变的。

②固定开关导通脉冲宽度ton不变，开关频率小于或等于谐振频率的二分之一，采用脉冲频率调制（PFM）改变开关的断开时间，电路维持在电流断续的工况，从而保持谐振条件的不变。

③一个开关周期的高频变压器的原边电流有效值随着开关频率的增大而增大，从而耦合到高频变压器副边的电流也随之增大，因此实现通过调节逆变器件的驱动脉冲周期来改变负载电容的充电电流。

3.谐振参数的计算

理论计算时，可以选取上面分析的四种模态中一种，列出微分方程，然后依据每一种模态的初始条件，求解微分方程就可以得到电感和电容值。这里给出工程上的一种计算方法。

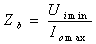(1).根据输入的直流电压、输出直流电流的变化，由下式求出基本阻抗Z_b为：

(3-1)

(2).根据变化器的容量和选择的开关器件，以及对体积、重量、可靠性和成本的要求，选择最高工作频率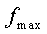，从而确定基本角频率_;

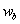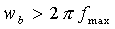                                   (3-2)

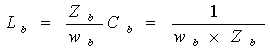(3).根据以下两式求基本谐振参数：

                                                   (3-3)

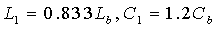(4).为了使变换器工作于电流断续工作模式，必须使得

                                                         (3-4)

谐振电感L1和谐振电容C1都是等效的参数，其中：

       前者是串联电感，后者是变压器以二次侧漏感之和（二次侧的经过折算）

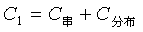     前者是串联电容，后者是电路中分布电容值。

经实际计算得到：L1=5mH,C1=2µF.

4.实验验证

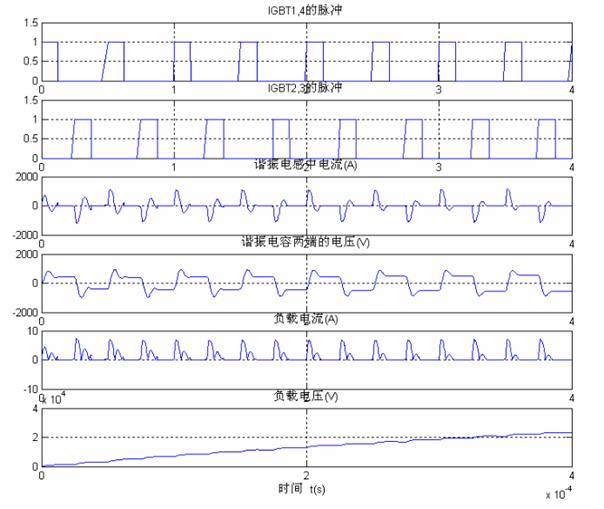
图 5 电流断续工作方式的主要波形

根据设计的谐振电感和电容值，可得到系统的串联谐振频率约为50kHz,由实验结果可以得到实际电源系统的谐振频率为66.7kHz,这是由于系统中脉冲变压器和寄生电感、分布电容以及开关器件的寄生电感和电容引起的。开关频率为20 kHz，保证了开关频率始终小于谐振频率的一半，整个电路电流始终工作于不连续导电模式。

由图5所示，电流波形趋近于正弦，在调频过程中，必须控制脉冲的关断时间在电流为负的时间里才能实现零电流关断，无法实现软开通。

5.小结

(1).结合课题本身，文中详细分析了单相全桥串联谐振软开关的工作原理以及谐振参数的计算。

(2).通过MATLAB软件仿真，证明了此方案的可行性并优化了方案的设计。

(3).应用串联谐振软开关技术的电源已经开发成功，并且已经有多台产品投入实际应用。

参考文献

[1].陈坚. 《电力电子学》   高等数学教育出版社   2002.1  .

[2].王兆安，黄俊. 《电力电子技术》第四版  机械工业出版社.

[3]. 王增福 李   魏永明编著，《软开关电源原理与应用》，北京，电子工业出版社，2006.4

[4] 王瑞华，脉冲变压器的设计，科学出版社出版，1987。