一种单相逆变电源的无差拍控制方法的研究
詹雄1,卢家林2,周玲玲1,苏彦民1,白小青2
(1西安交通大学,陕西 西安 710049)
(2西安爱科电子,陕西 西安 710045)
1 引言
随着高性能微处理器(如DSP)的出现,逆变电源的控制策略趋向于数字化。无差拍控制是一种数字控制方法,它较之其他的数字反馈控制方法具有更快的动态响应等优点。无差拍控制本质上要求脉冲宽度必须当拍计算当拍输出,但微处理器计算脉宽不可避免地引入计算延时,从而限制了脉冲宽度最大占空比。采用状态观测器对逆变器状态进行预估计可解决以上问题。因此,目前的无差拍控制大多是基于状态观测器的。然而状态观测器的参数是由主电路滤波器参数来决定的,因此,仅具有状态观测器的无差拍控制对主电路滤波参数变化比较敏感。为了让逆变电源适应各种不同类型的负载,不同形式的扰动观测器得到了深入的研究,但其算法大多比较复杂。
本文采用无差拍控制和传统的PI控制方法相结合的复合控制方法,既利用了无差拍控制的快速动态响应特性,又利用了PI控制具有较强的鲁棒性,据此设计的控制器能够使得逆变器的输出电压很好地跟踪参考正弦波,在电容性整流负载下输出电压也具有很好的正弦性,同时对主电路参数具有鲁棒性。本文首先详细地介绍了逆变电源系统模型的建立及控制算法的基本原理,然后在MATLAB/SIMULINK下建立了电源系统的仿真模型,完成了控制器的参数设计,并给出电源在不同负载下和主电路滤波器参数变化下的输出电压仿真波形,最后给出了一些有用的结论,对进一步的实验研究具有重要的指导意义。
2 系统模型及控制原理
2.1 系统模型
图1给出了单相逆变器的主电路结构和单个输出脉冲形式。
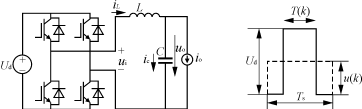
(a)主电路 (b)输出脉冲
图1逆变器电路拓扑结构及输出脉冲形式
根据图1(a),以滤波器电感电流iL(t)及电容电压uo(t)为状态变量,将负载电流io(t)当作扰动输入,则逆变桥输出滤波电路的状态方程为
 (t)=AX(t)+B1ui(t)+B2io(t) (1)
(t)=AX(t)+B1ui(t)+B2io(t) (1)
式中:
X(t)=[iL(t)uo(t)]T
A=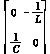 B1=
B1=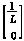 B2=
B2=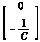
对ui(t)作不同的处理,则与式(1)对应的离散状态方程也有不同形式,此处,采用逆变电源的采样数据模型。为此,需假定每个采样周期Ts内ui(t)和io(t)保持不变。由于采样频率比较高,认为io(t)保持不变是合理的,而根据等效冲量原理,用ui(t)在一个采样周期内的平均值来代替该采样周期内的ui(t)值,如图1(b)所示。在以上假定下,式(1)可离散为
X(k+1)=ΦX(k)+Γ1u(k)+Γ2io(k) (2)
式中:
Φ=eATs= =
=
Γ1=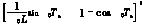 =
=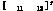
Γ2=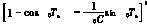 =
=
ω0=
u(k)=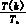 Ud
Ud
2.2 控制原理
本文所研究的逆变电源系统框图和控制律时序如图2所示。

(a) 逆变电源系统框图
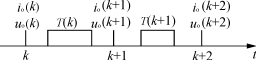
(b) 控制律时序
图2 逆变电源系统框图和控制律时序
为了构成反馈控制系统,需要检测若干逆变器主电路状态变量,这里检测负载电流和逆变器输出电压。为了对逆变电源输出电压进行控制,检测输出电压是必要的。之所以检测负载电流主要是考虑到今后逆变电源并联运行时的负载均流问题,此外它还可以使得逆变器适应各种负载。
由式(2)可得到
iL(k+1)=Φ11iL(k)+Φ12uo(k)+Γ11u(k)+Γ21io(k) (3)
uo(k+1)=Φ21iL(k)+Φ22uo(k)+Γ12u(k)+Γ22io(k) (4)
结合式(3)和式(4),并将uo(k+1),uo(k+2)分别用Vref(k+1),Vref(k+2)代替,可得到无差拍控制律
u(k+1)=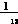 Vref(k+2)-
Vref(k+2)-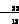 Vref(k+1)-
Vref(k+1)- iL(k)-
iL(k)-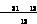 uo-
uo-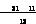 u(k)-
u(k)-
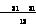 io(k)-
io(k)-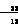 io(k+1) (5)
io(k+1) (5)
从式(5)可看出,如果io(k+1)及iL(k)也能求出,则u(k+1)就可求出。采用一个二阶预估方法对负载电流io(k+1)进行预估。
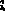 (k+1)=3io(k)-3io(k-1)+io(k-2) (6)
(k+1)=3io(k)-3io(k-1)+io(k-2) (6)
而iL(k)可由式(7)所示的关系求得。
iL(t)=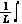 [ui(t)-uo(t)]dt (7)
[ui(t)-uo(t)]dt (7)
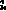 (k)=
(k)=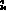 (k-1)+
(k-1)+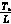
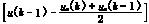 (8)
(8)
如果此时将式(5)中的io(k+1),iL(k)分别用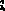 (k+1),
(k+1), (k)代替,求出控制律,那么该控制器将具有无差拍控制器所具有的缺点:对主电路参数敏感,抗扰动性较差。为此,引入PI控制,如图2(a)所示。
(k)代替,求出控制律,那么该控制器将具有无差拍控制器所具有的缺点:对主电路参数敏感,抗扰动性较差。为此,引入PI控制,如图2(a)所示。
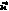 (k)=
(k)=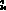 (k)-〔kp(Vref(k)-uo(k)〕+ki
(k)-〔kp(Vref(k)-uo(k)〕+ki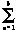 〔Vref(k)-uo(k)〕Ts (9)
〔Vref(k)-uo(k)〕Ts (9)
式中:kp,ki,为PI控制器参数,可通过仿真来确定。
将式(5)中的io(k+1),iL(k)分别用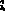 (k+1)和
(k+1)和 (k)代替,可得到最终控制律。算出控制量u(k+1)后,就可得到相应的脉冲宽度T(k+1)。
(k)代替,可得到最终控制律。算出控制量u(k+1)后,就可得到相应的脉冲宽度T(k+1)。
T(k+1)=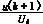 Ts (10)
Ts (10)
3 电源系统仿真模型的建立
在所研究的电源系统中,逆变电源主电路部分属于连续时间系统,而控制器部分则属于离散时间系统,因此,仿真模型也应属于连续与离散的混合模型,所选择的仿真软件工具要求能支持连续与离散时间系统的混合仿真。MATLAB就是这样一种仿真工具,本文就是在MATLAB/SIMULINK的环境下对所研究的电源系统进行建模的。
本文研究的逆变电源系统的仿真模型是基于传递函数的概念而建立的。将逆变电源主电路微分方程和离散控制律u(k+1)的表达式转化成相应的传递函数形式,就能得到如图3所示的仿真模型。这里,逆变器主电路的模型采用比较接近实际模型的采样模型,也就是说主电路滤波器输入ui(t)用每个开关周期内逆变桥臂输出电压的平均值来代替,同时假定功率开关器件为没有时间延时的理想开关。逆变电源所带的各种负载通过MATLAB中的S函数加以实现。在控制器模型的建立方面,值得注意的是应将系统中的离散模块的采样时间设置为电源系统的采样时间。用上升沿触发控制模块来模拟AD采样保持行为,实现对逆变器输出电压及负载电流进行采样,同时在控制量输出与逆变电源模型的输入量之间加了一个纯数字延迟模块,以表示微处理器计算驱动脉冲所带来的计算延时。
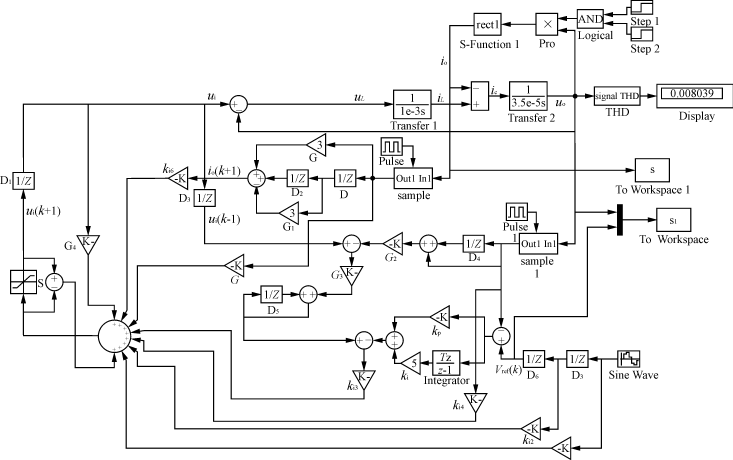
图3 基于MATLAB的逆变电源系统的仿真模型
在负载变化的情况下,无差拍控制方法下的控制量u(k+1)很可能超出逆变电源的直流母线电压,为此,要对u(k+1)进行限幅。加了限幅器之后,又可能带来非线性问题,因此,要对这种非线性进行补偿,一种简单有效的补偿方式如图4所示。
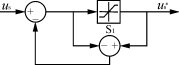
图4 限幅器的非线性补偿
4 仿真结果及分析
表1—表3列出了仿真时用到的主电路参数。需要说明的是由于该算法比较简单,如果采用高档单片机或DSP,完全有可能在25μs内完成所有控制算法,所以开关频率选择为40kHz。滤波电容电感的选择,要综合考虑滤波效果和滤波器所吸收的无功功率。
表1 主电路频率参数
| 输出电压频率/Hz
| 开关(采样)频率/kHz
|
| 50
| 40 |
表2 主电路电压参数
表3 主电路滤波器参数
根据表1—表3的参数,结合上面理论分析部分,可确定图3所示的仿真模型的大多数参数,剩下的未确定参数就是PI控制器的参数
kp,
ki。这两个参数可通过以下方法来确定:让逆变电源工作在突加突卸负载的状况下,并将突加突卸时刻点选择在输出电压的峰值处,首先将
kp取一个较小的值,然后逐渐增大
kp值,并同时观察输出电压波形,直到输出电压波形变得较差为止;
kp确定下来后,通过改变
ki值,并观察输出电压在突加突卸负载下的动态过程,直到得到满意的动态响应。通过以上步骤,最终选择
kp=0.4,
ki=5。
为了说明所设计的控制器的有效性,让逆变电源分别工作在阻性负载和电容性整流负载的状况下。图5和图6分别是以上两种情况下输出电压uo,输出电流io及参考正弦信号Vref的仿真波形。可以看出所设计的逆变电源系统能较好地适应各种负载。
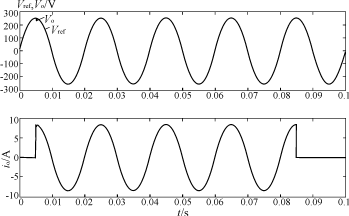
图5 逆变电源在100%突加/卸阻性负载(R=30Ω)下的波形
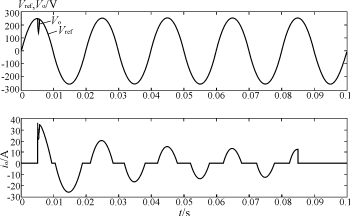
图6 逆变电源在100%突加/卸电容性整流负载(C=2200μF,R=40Ω)下的波形
为了验证控制器具有一定的鲁棒性,改变滤波器电路参数,观察仿真实验波形。可以发现,如果滤波电容值保持为设计值,滤波电感值在95%~105%范围变化时,逆变电源输出电压在整流性负载下仍能很好地跟踪参考正弦信号。如果滤波电感值保持为设计值,滤波电容值在87.5%~175%范围变化时,输出电压也能很好地跟踪参考信号。图7,图8分别给出了滤波电感减少5%和滤波电容减少12.5%时的仿真波形。
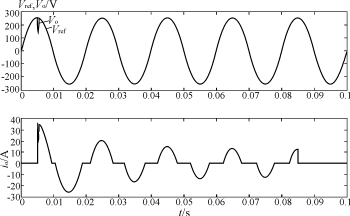
图7 滤波电感减少5%时的仿真波形
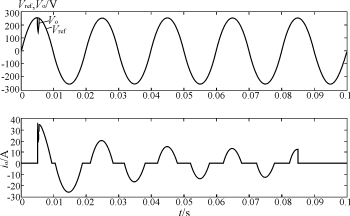
图8 滤波电容减少12.5%时的仿真波形
5 结语
本文详细地介绍了逆变电源无差拍控制方法和传统PI控制方法相结合的复合控制方法基本原理,在此基础上建立了逆变电源系统的仿真模型,在仿真过程中确定了PI控制器参数值,从而完成了整个控制器的设计。逆变电源在不同负载情况下的仿真波形,说明了所设计的电源系统抗负载扰动能力强;在主电路滤波器参数发生变化时的仿真波形,说明了所设计的系统对参数具有一定的鲁棒性。由于该电源输出电压能很好地跟踪输入参考正弦波,因此可以实现多台逆变电源的并联运行。
