三相PFC电路的交流侧输入电感谐波电流注入方案

董晓伟  曹建安  裴云庆  西安交通大学(西安 710049)

摘  要：随着电力电子技术的发展，大量电力电子装置的使用，产生的谐波电流严重影响了电能质量。因此功率因数校正技术也得以发展，而且针对不同的电路拓扑已经有很多控制方案。本文针对三相功率因数校正电路拓扑，介绍了一种在其交流测输入电感进行谐波注入的控制方案，来达到比较好的抑制谐波效果。

关键词：谐波  功率因数校正  谐波注入

Current injection of AC side inductor for three-phase PFC circuit

Abstract: The last years, with the developing of the power electronics technology, many power electronics devices are used. And this engenders many harmonics, the harmonics affect the quality of electric energy. So the power factor correction is developed, and there have many control projects that suit with different circuits. This article introduces a control project, this project injects harmonic current into inductor on the AC side, it suits for the three-phase PFC circuit.

Keyword: harmonic  power factor correction  harmonic injection

1  前  言

随着电力电子装置应用的日益增多和装置容量的不断加大，装置所产生的谐波污染问题日益受到关注。功率因数校正技术是改善谐波的根本手段。单相功率因数校正技术目前已经实用化，三相功率因数校正技术虽也有应用，但如何提高其性能、降低成本仍为研究的热点。在双开关三相三线PFC(Power Factor Correction)电路拓扑中，目前国际上研究比较多的三相三线PFC谐波电流注入方案[1][2]，主要是以Mohan等学者提出的，将滤波电感放在直流侧的双升压电路型三相PFC电路。该方案和优化的谐波电流注入法相结合，可以将三相电源的输入电流校正成正弦波，使三相电源系统达到单位功率因数。采用不同的谐波电流注入方案以及不同的电流反馈方案，对输入电流的谐波含量都有很大的影响。因为三相整流桥中的每个二极管，很难导通180°，二极管的利用率低，电流的有效值较大，损耗高。为此作者提出了将电感串联在交流侧的电路拓扑，其结构如图1所示。本文将对该在此电路中将三相四线PFC电路拓扑中性线的3次谐波电流通过一个滤波器注入到三相电网中，消除中性线的3次谐波电流，从而省掉了中性线。

图1  三相三线PFC电路拓扑

但是无论采用什么样的控制方案，当输出功率恒定时，二极管电流的有效值总是大于二极管工作在180°的时候。而且电感串联在直流侧时，其电流指令的获取比较困难，要通过电网电压信号的多次运算，才能得到。只有将输入滤波电感，并且控制二极管导通180°，才有可能提高。

2  理论分析

三相三线PFC电路拓扑中，在每一相电感电流都存在着不可控区间。而且，该区间的电流峰值与输入电压、输出电压、输入电感以及占空比等相关，因此，本文首先研究了不可控区间的电流，然后求解出当三相输入电流为正弦波形时，三个输入电感的电流波形。

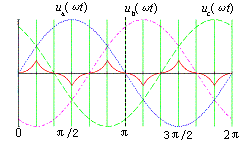
图2  三相输入电压波形的12个区间

2.1  不可控电流的分析

设输入电压为对称的三相电压ua(ωt)、ub(ωt)和uc(ωt)，为了描述方便，画三相电压波形如图2所示，并且以a相电压正向过零点为相位起始点。将一个工频周期[0，2π]平均分为12个区间，在[0，π/6]、[5π/6，π]、[π，7π/6]、[11π/6，2π]区间a相电压低于c相或者b相电压，因此a相电流不可控。在[0，π/6]区间a相一个开关周期的平均电流ia1(ωt)表示为：

(1)

该区间的电流波形如图2中[0，π/6]区间所示。

在[5π/6，π]区间a相一个开关周期的平均电流ia6(ωt)表示为：

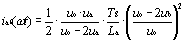(2)

由上两个式子表明，当三相电压对称时，a相在两个[0，π/6]和[5π/6，π]的电流以π/2为轴对称。如果设a相在[0，π/6]区间的电流波形为f(ωt)，则a相在[0，2π]工频周期的不可控区间电流表示为：

(3)

同理，可以得出其他两相在[0，2π]工频周期的不可控区间电流ib(ωt)和ic(ωt)分别为：

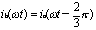	(4)

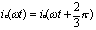对于三相电源而言，设三相不可控总电流为ih(ωt)，即有：

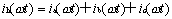(5)

那么，该电流的波形如图3所示。将ih(ωt)进行Fourier分解：

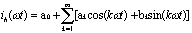(6)

其中

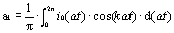
图3  三相不可控电流总和

由图3可见，该电流ih(ωt)的波形为奇函数，关于起始点对称，即：

(7)

故                                          

ak＝0（k=0,1,…）

同时，该函数具有镜对称性质，即：

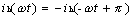(8)

故                                             

a2k＝b2k＝0（k=1,2,…）

现在，ih(ωt)的Fourier级数只有正弦项的奇次频率项系数。经对上式积分可得：

(9)

对于工频而言，上式说明：不可控电流总和是三相电源的总零序电流，并且不含有非零序电流；而且，该式表明，ih(ωt)的大小和形状不影响其频谱分布，只影响其某频率的幅值大小。该函数的频谱如图4所示。

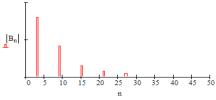
图4  不可控总电流频谱

2.2  电感电流iLa(ωt)的计算

以a相电流为例，a相不可控部分电流如式(3)所表示。如果将a相电流可控部分[π/6，5π/6]和[7π/6，11π/6]区间的电流波形控制成正弦波的一部分，而将a相不可控区间的电流补偿成正弦波形，那么，该区间应该补偿的电流ian(ωt)为：

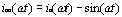(10)

同理，可以得到b相和c相在各自的不可控区间的补偿电流分别为：

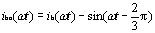	(11)
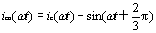	(12)

同样将三相的补偿电流合成为i0(ωt)，即：

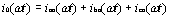(13)

根据上述函数，合成电流i0(ωt)的波形如图5所示。对该电流进行Fourier分解，得到其频谱，如图6所示。由图可见，该补偿电流也只含有零序电流。

图5  合成的补偿电流

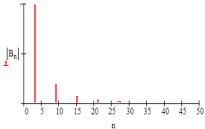
图 6  合成补偿电流频谱

为了使三相输入电流为正弦波，将补偿电流i0(ωt)注入到三相电网中，就可以使三相各自不可控区间的电流补偿成正弦波形。那么，a相可控区间的电流ia2~5(ωt)为：

这样，该式和式(3)合在一起，成为a相输入电感电流完整的正半周波形。同样，能够得到a相负半周的电流波形。所以，a相输入电感电流iLa(ωt)的完整表达式为：

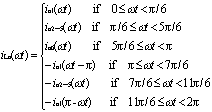(15)

a相电感电流iLa(ωt)的波形如图 7所示，其电流频谱如图8所示。同样，其他两相的电感电流波形也可以得到，只是和a相电流相位差2π/3。

图7  a相电感电流波形

由图 7可见，三相电感电流在一个工频周期总是连续的。应用三相三线PFC电路拓扑，可以使每个整流桥二极管能够在半个周期内全部导通，这样有利于提高二极管的利用率；同时，在输出同样的功率情况下，可以降低二极管的峰值电流；降低了开关管工作的峰值电流；降低了零序注入电流的峰值，可以使用较小功率的工频变压器将零序分量分别注入到三相电源中。

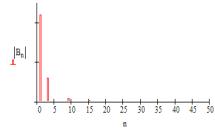
图8  a相电感电流波形频谱

现在，三相的电感电流iLa(ωt)、 iLb(ωt)、 iLc(ωt)已经知道，工频变压器注入的零序电流i0(ωt)也已经得到了。那么，三相的输入电流为：

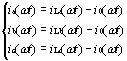(16)

于是，该三相三线PFC电路拓扑的三相输入电流如图9所示，图10为其电流频谱，可见其输入电流为正弦波形，不含有任何谐波分量。

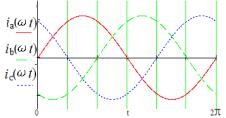
图9  三相电源电流波形

3  结  论

综上所述，对于三相三线PFC电路拓扑，利用交流侧输入电感的谐波电流注入方案可以达到比较理想的功率因数校正效果，而且具有以下优点：

(1) 输入电网电压对称的情况下，三相输入电流为正弦波，输入电流不含有谐波，可以达到单位功率因数。

图10  三相电源电流波形频谱

(2) 开关管的峰值电流较小，能够降低导通损耗；二极管的导通角达到180°，提高了二极管的利用率。

参考文献：

[1] Naik R., Rastogi M., Mohan N., Nilssen R., Henze C.P., “A magnetic device current injection in a three-phase sinusoidal-current utility interface”. Industry Applications Society Annual Meeting, 1993, Conference Record of the 1993 IEEE, 1993 Page(s): 926 -930 vol.2

[2] Yungtaek Jang and Milan M.Jovanovic, “A Novel, Robust, Harmonic injection method for single-switch, three-phase, discontinuous- conduction-Mode boost rectifiers”. IEEE PECS’97 Record, pp.469-475.st.louis.Mo, June 22-27, 1997.

[3] 裴云庆，段雅莉，王兆安，“具有参数优化功能的电力电子系统CAD软件PECS3.2”，第八届全国自动化电控系统学术年会论文集，成都，1996

[4] 王兆安，杨君，刘进军等，谐波抑制和无功功率补偿。机械工业出版社，1998

[5] 王兆安，黄俊，电力电子技术。第4版.机械工业出版社，2000

[6] Takeda M., Ikeda K., Tominaga Y., “Harmonic current compensation with active filter”. Proc of IEEE/IAS Annual Meeting, 1987. 808~815